はじめに
楽曲分析では、メロディー、ハーモニー、リズムの3大要素から特徴を捉えるのが大事です。
ハーモニーに関しては、音楽理論による体系化(コード、コード進行など)が出来ていることもあり、計算機による分析も他の要素よりも普及しています。
一方で、特にリズムに関する分析は、ハーモニーのそれと比べるとWeb上には情報が少ないです。
そこで、この記事では、局所/大域のテンポ分析やBPM算出で使われる、テンポグラム (Tempogram)について、Pythonのコードとともに紹介します。実装と理解の助けになれば幸いです。
テンポグラムとは
図のように、テンポグラムは時間-テンポ (BPM, または周波数, 周期) 表現であり、局所的なテンポを分析するのに使われます。
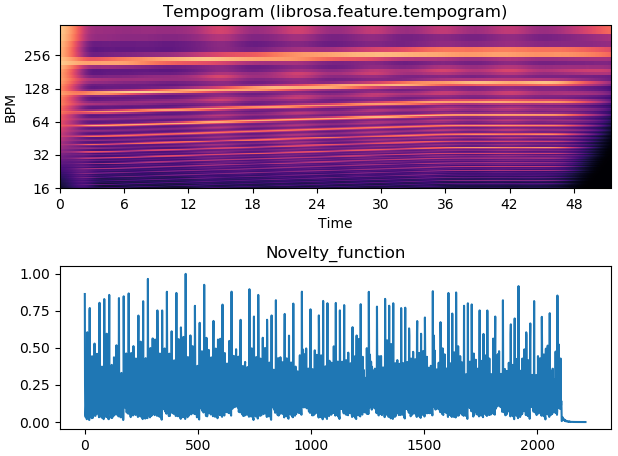
なお、テンポグラムの算出には、元の楽曲信号ではなく、発音タイミングが分かりやすいように加工した信号 Novelty function を使います。 Novelty functionについては、以下の記事でまとめています。
テンポグラムにはいくつか種類があるため、それらを算出方法とともに紹介したいと思います。
各テンポグラムの紹介と実装
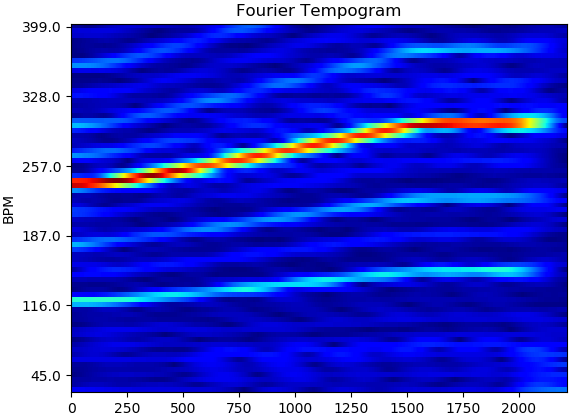
フーリエテンポグラム (Fourier Tempogram)
フーリエテンポグラムは、Novelty function に対して短時間フーリエ変換を適用して得られた振幅スペクトログラムです。つまり、Novelty function を時間信号とみなして、短い時間区間ごとに周期分析をしています。
def compute_fourier_tempogram(novelty_function, sr, hop_length, n_fft_tg, hop=10): ftg = np.abs(librosa.stft(novelty_function, hop_length=hop, n_fft=n_fft_tg)) sr_novfunc = sr / hop_length # hop_length = 512 sr_novfunc_minite = 60 * sr_novfunc ftg_bpms = np.linspace(0, float(sr_novfunc_minite) / 2, int(1 + n_fft//2), endpoint=True) return ftg, ftg_bpms
サンプリング周波数が sr の楽曲信号より、hop_length=512 サンプルから1点を算出したnovelty_functionを用いて、フーリエテンポグラムを計算するとします。すると、novelty_functionのサンプリング周波数はsr/hop_length となります。ここで、srが毎秒なのに対してBPMは毎分であるため、短時間フーリエ変換後の各周波数ビンは、コード中のbpms に対応します。
なお、STFTでは hop_length=1 となっていることに注意してください。計算量と解像度のトレードオフを考慮して小さい値を設定します。
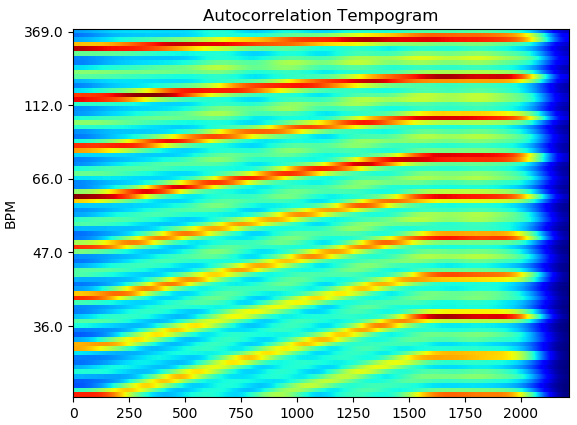
自己相関テンポグラム (Autocorrelation Tempogram)
自己相関テンポグラムは、Novelty function のある短い時間区間ごとに自己相関関数を計算することで得られますです。自己相関はピッチ推定などでも用いられる手法です。
自己相関の算出には、Wiener–Khinchin 定理を用いた効率的な計算方法が良く使われます。Novelty function の短い時間区間ごとに、FFT でパワースペクトルを得て、それを逆 FFT することで自己相関を算出します。(信号のパワースペクトル=自己相関関数のフーリエ変換であるため。)
def compute_autocorrelation_tempogram(novelty_function, sr, hop_length, n_fft_tg, hop=10): PS = np.abs(librosa.stft(novelty_function, hop_length=hop, n_fft=n_fft_tg)) ** 2 n_bpm_freq, n_bpm_t = PS.shape actg = np.zeros((n_bpm_freq-1, n_bpm_t)) for t in range(0, n_bpm_t): actg[:,t] = np.fft.irfft(PS[:,t], axis=0)[1:n_bpm_freq] sr_novfunc = sr / hop_length actg_bpms = 60 * sr_novfunc / np.arange(1, n_bpm_freq) actg, actg_bpms = actg[::-1], actg_bpms[::-1] return actg, actg_bpms
テンポグラムのBPM範囲を限定
上記のテンポグラムの計算では、30以下のBPMや、1000以上のBPMも算出しています。後段の計算の際にノイズとなる可能性があるため、bpm_min から bpm_maxまでの範囲のみ、計算で用いることにします。
次の adjust_tempogram() は、指定されたBPMの範囲内のテンポグラムを返す関数です。
def adjust_tempograms(tg, bpms, bpm_min, bpm_max): indices = np.where(np.logical_and(bpms>=bpm_min, bpms<=bpm_max))[0] return tg[indices], bpms[indices]
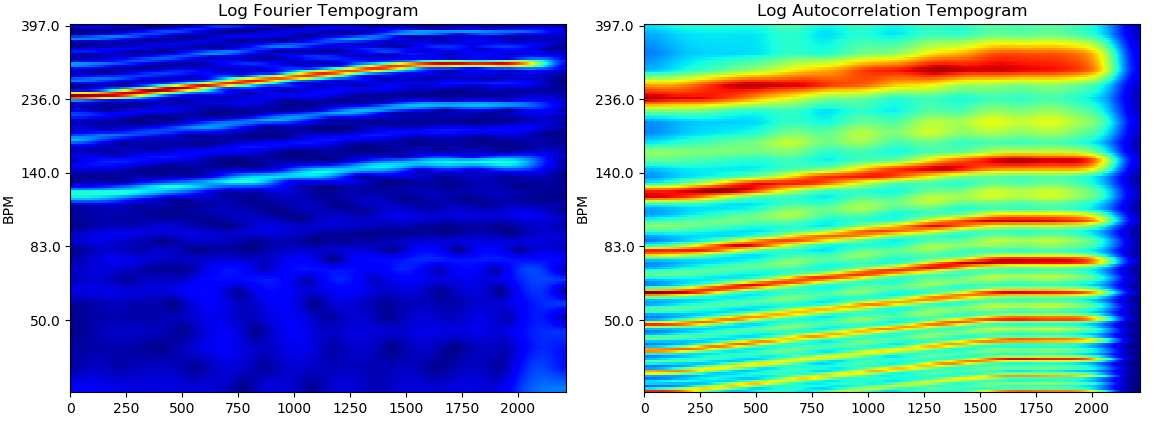
対数テンポグラム
周波数・ピッチ分析では、調波構造(倍音)や音高の関係を分かりやすく可視化するため対数軸をよく使います。 同様に、テンポ分析でも対数軸のほうが都合が良く、また、サイクリックテンポグラムの計算で利用するので、対数テンポグラムを算出します。
ピッチ分析の時と同じく対数軸への変換方法はいくつかありますが、以下の実装では線形補完によって対数化しています。
# Compute log tempogram with linear interpolation def compute_log_tempogram(tg, bpms, tempo_ref=30, oct_bin=36, oct_num=4): from scipy.interpolate import interp1d log_bpms = tempo_ref * 2 ** (np.arange(0, oct_num*oct_bin)/oct_bin) log_tg = interp1d(bpms, tg, kind='linear', axis=0, fill_value='extrapolate')(log_bpms) return log_tg, log_bpms
サイクリックテンポグラム (Cyclic Tempogram)
フーリエ/自己相関テンポグラムを見ていると、通常の短時間フーリエ変換や定Q変換と同じく、規則的な縞模様の存在に気づきます。これは、BPMにおける高調波(整数倍音)と低調波(分数倍音)です。
そこで、以下の論文では、音高からクロマ特徴を得る時に用いる対数周波数表現上での巡回を応用したテンポ特徴表現手法であるサイクリックテンポグラムが提案されています。
簡単に言えば、半テン・倍テンなどの成分をひとまとめにしています。クロマ特徴で同じ音高記号の音(例:...C3, C4, C5, ...)をまとめているのと同じです。
例えば、元のテンポグラム T からBPM=[..., 30, 60, 120, 240, 480]に関するサイクリックテンポグラムの成分 C を算出するには、
C= ... + T[BPM=30] + T[BPM=60] + T[BPM=120] + T[BPM=240] + T[BPM=360] + ...
というように、2のべき乗 * BPM でまとめます。以下、実装と適用結果です。
def compute_cyclic_tempogram(tg, bpms, tempo_ref=30, oct_bin=36, oct_num=4): # Compute log tempogram log_tg, log_bpms = compute_log_tempogram(tg, bpms, tempo_ref, oct_bin, oct_num) n_bpms, n_t_tg= log_bpms.shape[0], log_tg.shape[1] # Compute cyclic tempogram ctg = np.zeros((oct_bin, n_t_tg)) for m in np.arange(0, oct_bin): ctg[m,:] = np.mean(log_tg[m:n_bpms:oct_bin,:], axis=0) ctg_sf = 2 ** (np.arange(0, oct_bin)/oct_bin) return ctg, ctg_sf
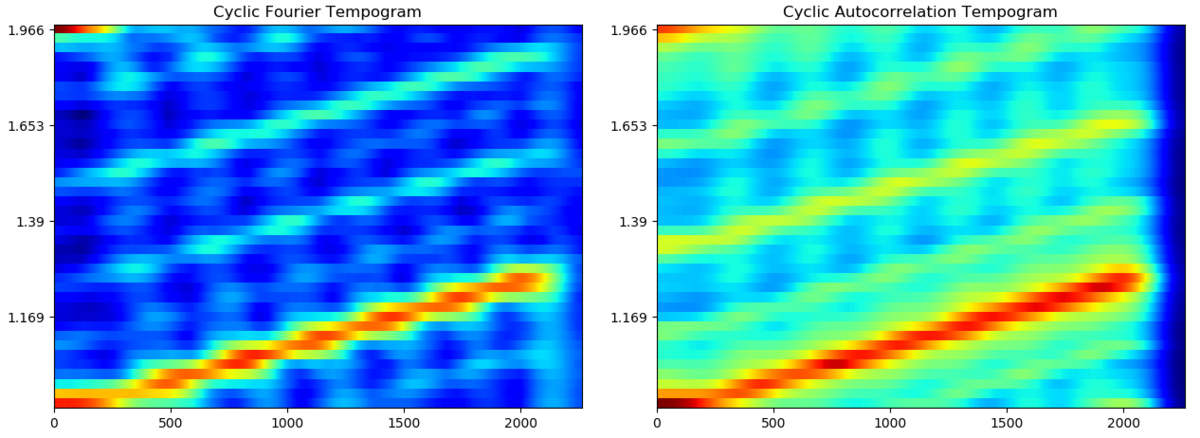
サイクリックテンポグラムは、クロマベクトルと同じように、時間方向に合算してヒストグラムを楽曲特徴ベクトルとしたり、あるいは、そのまま特徴量としてニューラルネットに入力したりするのが良さそうです。
活用例
BPM算出
Pythonの音楽情報処理ライブラリ "LibROSA" のBPM算出では、テンポグラムを元に楽曲全体のBPMを推定するような実装になっています。
テンポグラムを特徴量とした音楽分析
参考文献
- http://mac.citi.sinica.edu.tw/~yang/teaching/lecture12_tempo_beat_rhythm.pdf
- C6S2_TempogramAutocorrelation
- C6S2_TempogramCyclic
補足
LibROSA のテンポグラムについて
LibROSAの librosa.feature.tempogram() は自己相関テンポグラムとなっています。なお、フーリエテンポグラムも librosa.feature.fourier_tempogram() として実装されています。
BPM算出の際は、librosa.beat.tempo()の実装のように、テンポグラムの時間方向ヒストグラムを作り、それに周波数重み付けをして、最大値に対応するBPMを推定BPMとして算出するのがよいと思います。(重み付けをしないと、低/高調波の影響で倍・半テンポがBPM推定値として算出される可能性があります。)
実験に使った音源
BPM=120からBPM=150まで、時間とともにBPMが上がるような音源です。Image-line社のソフトウェアシンセ "Harmor" のプリセット "Nyan Cat"を利用しています。
Spectral based novelty function
def compute_spectral_based_novelty(y, hop_length): Y = np.log(np.abs(librosa.stft(y))+1) n_freq, n_tf = Y.shape spectral_novelty = np.zeros(n_tf-1) # Compute and accumulate novelty function each frequencies for f in range(0, n_freq): tmp = Y[f,1:] - Y[f,:-1] tmp[tmp<0.0] = 0.0 spectral_novelty += tmp # Normalization spectral_novelty /= np.max(spectral_novelty) return spectral_novelty
プロットに用いたコード
filepath = librosa.util.example_audio_file()
filepath = "audio_example_bpm.mp3"
y, sr = librosa.load(filepath, sr=16000)
# Spectral based novelty curve
hop_length = 512
novelty_function = spectral_based_novelty(y, hop_length)
# Compute Fourier tempogram
n_fft = 512
bpm_min, bpm_max = 30, 480
tg, tg_bpms = compute_fourier_tempogram(novelty_function, sr, hop_length, n_fft)
tg, tg_bpms = adjust_tempograms(tg, tg_bpms, bpm_min, bpm_max)
log_tg, log_tg_bpms = compute_log_tempogram(tg, tg_bpms)
ctg, ctg_sf = compute_cyclic_tempogram(log_tg, log_tg_bpms)
__plot_tg(tg, tg_bpms, context="Fourier Tempogram")
__plot_tg(log_tg, log_tg_bpms, context="Log Fourier Tempogram")
__plot_ctg(ctg, ctg_sf, context="Cyclic Fourier Tempogram")
# Compute Autocorrelation tempogram
n_fft = 512
bpm_min, bpm_max = 30, 480
tg, tg_bpms = compute_autocorrelation_tempogram(novelty_function, sr, hop_length, n_fft)
tg, tg_bpms = adjust_tempograms(tg, tg_bpms, bpm_min, bpm_max)
log_tg, log_tg_bpms = compute_log_tempogram(tg, tg_bpms)
ctg, ctg_sf = compute_cyclic_tempogram(log_tg, log_tg_bpms)
__plot_tg(tg, tg_bpms, context="Autocorrelation Tempogram")
__plot_tg(log_tg, log_tg_bpms, context="Log Autocorrelation Tempogram")
__plot_ctg(ctg, ctg_sf, context="Cyclic Autocorrelation Tempogram")
def __plot_tg(tg, bpms, context="Tempogram", ticks_base=10, filepath=None): plt.clf() plt.imshow(tg[::-1], aspect="auto", cmap="jet") plt.colorbar() plt.title(context) plt.ylabel("BPM") ticks = 2 * (len(bpms) // ticks_base) plt.yticks(np.arange(0,len(bpms), ticks), np.round(bpms[::-1][::ticks], 3)) pltsave(filepath, "tempo_tg") def __plot_ctg(ctg, ctg_sf, context="Cyclic Tempogram", filepath=None, ticks=5): plt.clf() plt.imshow(ctg[::-1], aspect="auto", cmap="jet") plt.colorbar() plt.title(context) plt.yticks(np.arange(0,len(ctg_sf), ticks), np.round(ctg_sf[::-1][::ticks], 3)) pltsave(filepath, "tempo_ctg")