音楽の分析方法としてBPM・テンポの分析は非常に重要です。
BPM・テンポの分析を行うことで、楽曲の雰囲気、ノリ、音楽ジャンルといった全体的な特徴を捉えることができます。
BPM・テンポの分析方法としては、テンポグラムという便利な手法があります。
テンポグラムの実装は結構難しいですが、Pythonであれば音楽分析ライブラリ LibROSA を使うことで数行で算出することができます。
そこで、この記事では LibROSAを使ったテンポグラムの算出方法を紹介します。
LibROSAでのテンポグラム算出方法
テンポグラムは時間-テンポ (BPM) の行列であり、楽曲の全体的・局所的なテンポ・BPMを分析するのに使われます。
テンポグラムにはフーリエテンポグラムと自己相関テンポグラムという2つの手法がよく知られています。それぞれ特徴があるので,やりたい分析や対象信号に応じて使い分けていくのがよいと思います。
なお、LibROSAではどちらのテンポグラムも実装されており気軽に利用することができます。
フーリエテンポグラム、自己相関テンポグラムそれぞれの算出・実装方法は以下の記事にまとめていますので、ご興味がありましたらお読みください。
以下では、LibROSAのフーリエテンポグラム、自己相関テンポグラムの使い方についてみていきます。
LibROSA テンポグラム
LibROSAのフーリエテンポグラム、自己相関テンポグラムはどちらも同じような引数であるため、まとめて説明します。
librosa.feature.tempogram(y=None, sr=22050, onset_envelope=None, hop_length=512, win_length=384, center=True, window='hann', norm=inf)
librosa.feature.fourier_tempogram
librosa.feature.fourier_tempogram(y=None, sr=22050, onset_envelope=None, hop_length=512, win_length=384, center=True, window='hann')
重要な引数:
- y: モノラルの時間信号
- sr: サンプリング周波数
- onset_envelope:
- オンセットエンベロープ
- 2次元の場合、最初の1次元ごとにテンポグラムを算出
- hop_length:
- どのくらい信号をずらしながらテンポグラムを算出するか
- win_length:
- フーリエ変換や自己相関を算出する信号の長さ
- デフォルト:384 * hop_length / sr ~= 8.9秒
必ず必要な引数は以下のどちらかです。
y,srを与えるonset_envelopeを与えるの場合、
tempogram()内部でonset_envelopeを計算します。
オンセットエンベロープは、発音タイミングを抽出した信号です。楽曲の時間信号はそのまま使うとテンポ・リズム分析しにくいので、拍検出やリズム分析ではこのオンセットエンベロープが良く利用されます。
Librosaではオンセットエンベロープを抽出できる関数librosa.onset.onset_strength() が実装されているので、1行で算出できます。
詳細は以下の記事を参考にしてください。
サンプルコード
# -*- coding: utf-8 -*- import sys import numpy as np import librosa import librosa.display import matplotlib.pyplot as plt sr = 22050 hop_length = 512 filepath = sys.argv[1] y, sr = librosa.load(filepath, sr=sr) #y, sr = librosa.load(librosa.ex('choice')) # オンセット包絡線の算出 onset_envelope = librosa.onset.onset_strength(y=y, sr=sr, hop_length=hop_length) # フーリエテンポグラム fourier_tempogram = librosa.feature.fourier_tempogram( onset_envelope=onset_envelope, hop_length=hop_length ) # 自己相関テンポグラム autocorr_tempogram = librosa.feature.tempogram( onset_envelope=onset_envelope, hop_length=hop_length ) # プロット plt.subplots(figsize=(8.0, 4.0)) plt.subplot(1,2,1) librosa.display.specshow(np.abs(fourier_tempogram)**0.5, sr=sr, hop_length=hop_length, x_axis='time', y_axis='fourier_tempo', cmap='jet') plt.title('Fourier tempogram') plt.subplot(1,2,2) librosa.display.specshow(np.abs(autocorr_tempogram), sr=sr, hop_length=hop_length, x_axis='time', y_axis='tempo', cmap='jet') plt.title('Autocorrelation tempogram') plt.tight_layout() plt.show()
プロット例
米津玄師の楽曲でテンポグラムを算出してみました。
Lemon (BPM=87)

パプリカ (BPM=103)
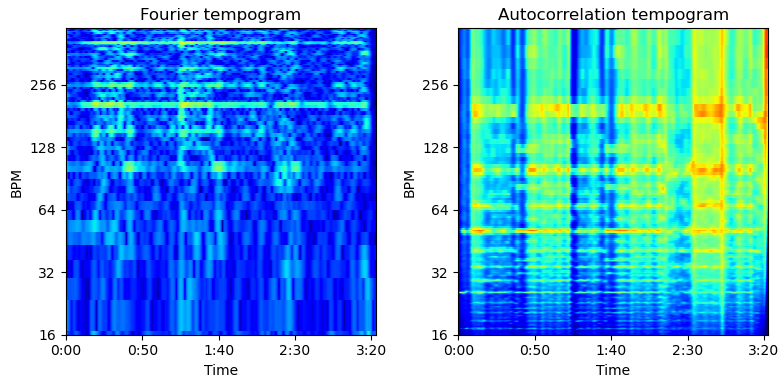
ゴーゴー幽霊船 (BPM=180)

まとめ
LibROSAを使ったテンポグラムの算出方法を紹介しました。
なお、BPM・テンポ分析の精度や品質を上げる方法としては、テンポグラムに与える信号を加工することが考えられます。
例えば、低域/高域通過フィルタや、調波打楽器音分離 (HPSS) が有効です。
また、テンポグラムからBPMを推定することも可能であり、実例としてLibROSAのBPM推定ではテンポグラムが使われています.