
前回の記事では,音楽信号の音高分析に便利な定Q変換 (CQT)のアルゴリズムや実装方法による計算速度の比較を行いました。
結果として,再帰的ダウンサンプリング法による定Q変換がリアルタイム処理で実用的な計算速度であることが分かりました。
しかし、アルゴリズムは同じでもバッチ処理向けの実装である librosa.cqt が圧倒的に速い結果になりました。
そこで、今までリアルタイム処理用に実装してきた再帰的ダウンサンプリング法による定Q変換で、バッチ処理用の実装をすることで、LibROSA の定Q変換くらいの計算速度となるのか試してみました。
実装方法
定Q変換のアルゴリズムの原理は以下の記事を参考にしてください。
また、この実装は再帰的ダウンサンプリング法による定Q変換 がベースとなっていますので、そちらも合わせてお読みいただければ幸いです。
リアルタイム処理向け実装が遅い理由
リアルタイム処理の場合、次々とやってくる 0.05 ~ 0.1 秒ほどの入力信号フレームに対して逐次処理する必要があります。
再帰的ダウンサンプリング法による定Q変換の場合、入力信号に対して低域通過フィルタ→間引き処理(=ダウンサンプリング)を行う必要があります。
従って,リアルタイム処理向けの定Q変換では、毎フレームダウンサンプリング処理をしなければなりません。
一方で,バッチ処理であれば入力として信号全体が一度に与えられます。
そのため、バッチ処理では時間方向の処理を一括で行うことができます。
その計算時間の差は実装方法、計算機環境、プログラミング言語処理系次第ですが、経験的にPythonで信号処理をする場合は実装方法の違いで大きく変わる印象です。
バッチ処理向け実装
以下のような方針で実装しました。
- 信号全体に対して再帰的ダウンサンプリングを行う
x: 入力信号xd_raw:xをダウンサンプリング した信号- [ダウンサンプリング1回の信号,ダウンサンプリング2回の信号,…,ダウンサンプリングN回目の信号]を格納するリスト
- ダウンサンプリングされた信号からスペクトル算出に使う信号を切り出す
- スペクトルカーネルを使ってCQTスペクトルを計算
再帰的ダウンサンプリング法の実装し始めは、
xd_rawとxdの違いが分かりにくかったです。
xdはxd_rawの一部を切り出していることに注意してください。
def stcqt_batch(self, x): n_frames = len(x) // self.hop_length n_x_adjust = 2 ** (self.n_octave-1) n_pad = n_x_adjust - (len(x) + self.n_fft) % n_x_adjust len_x = len(x) + self.n_fft + n_pad # 1. recursive downsampling xd_raw = np.zeros((self.n_octave, len_x)) tmp_x = np.zeros(len_x) xd_raw[0, 0:len(x)] = x[:] for k in range(1, self.n_octave): idx1 = len_x // 2 ** (k-1) idx2 = idx1 // 2 tmp_x[0:idx1] = filtfilt(self.lpf_b, self.lpf_a, xd_raw[k-1, 0:idx1]) #lfilter xd_raw[k, 0:idx2] = tmp_x[0:idx1][::2] #xd_raw[k, 0:idx2] = resampy.resample(xd_raw[k-1, 0:idx1], self.sr/ 2**(k-1), self.sr/ 2**k, filter='kaiser_fast') # 2. make xd xd = np.zeros((self.n_octave, n_frames, self.n_fft_1oct)) _batch_make_xd(xd_raw, xd, self.n_octave, self.n_bpo, n_frames, self.n_fft, self.n_fft_1oct, self.hop_length) del xd_raw, tmp_x # 3. calc. cqt-spec using spectral kernel by each octave spec = np.zeros([self.n_pitch, n_frames], dtype=np.complex128) xd_fft = np.zeros(self.n_fft_1oct, dtype=np.complex128) for k in range(0, self.n_octave): st = self.n_bpo * (self.n_octave-k-1) en = st + self.n_bpo for n in range(n_frames): xd_fft[:] = np.fft.fft(xd[k, n, :]) spec[st:en, n] = np.dot(self.spectral_kernel, xd_fft) return spec
@jit('void(f8[:,:], f8[:,:,:], i8, i8, i8, i8, i8, i8)', nopython=True, nogil=True) def _batch_make_xd( xd_raw, xd, n_octave, n_bpo, n_frames, n_fft, n_fft_1oct, hop_length, ): for k in range(0, n_octave): center_init = n_fft // 2 ** (k + 1) hop_length_ds = hop_length // 2 ** k for n in range(n_frames): center = center_init + n * hop_length_ds st = center - n_fft_1oct//2 en = center + n_fft_1oct//2 xd[k, n, :] = xd_raw[k, st:en]
ソースコード
ベンチマーク
比較環境
- OS: Win10
- Python環境: Anaconda

その他の条件は、リアルタイム向け実装のベンチマークの記事を参考にしてください。
90秒の信号,12ビン/1オクターブ
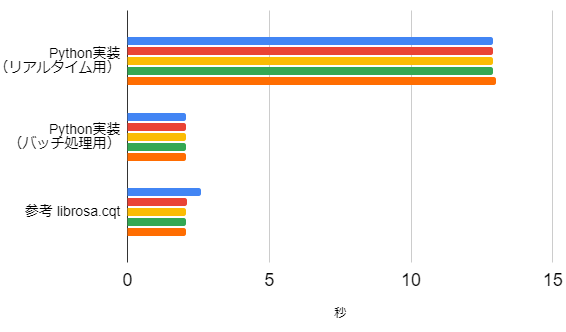
90秒の信号,24ビン/1オクターブ
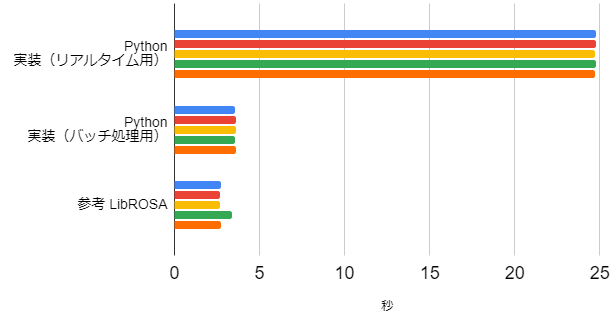
5分(300秒)の信号,12ビン/1オクターブ
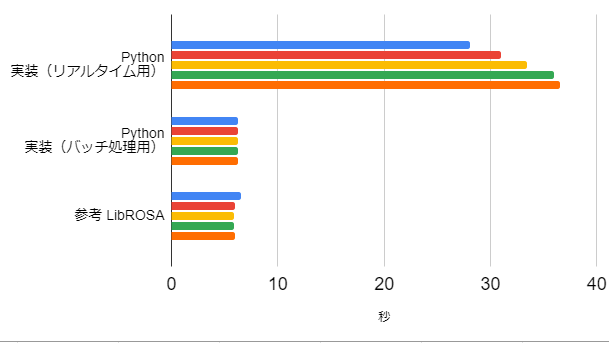
5分(300秒)の信号,24ビン/1オクターブ
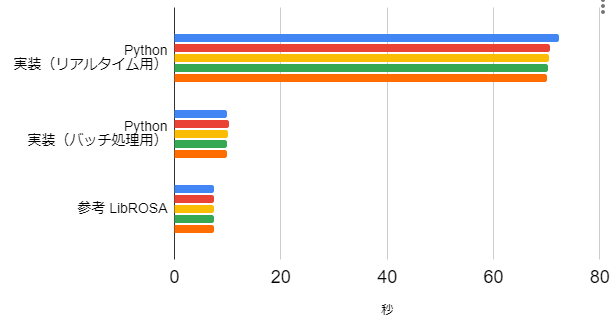
まとめ
再帰的ダウンサンプリング法による定Q変換のバッチ処理向け実装と、そのベンチマーク結果を紹介しました。
リアルタイム実装と比べると5~7倍くらい速くなり,LibROSAの定Q変換と同じくらいの計算速度となりました。
ただ、1オクターブ中のビン数が増えるとLibROSAの計算速度の速さが目立ちました。その計算・実装の工夫が分かったら、また別途まとめたいと思います。