はじめに

音信号の時間周波数分析にはFFT (高速フーリエ変換) ／STFT（短時間フーリエ変換）がよく使われます．

しかし，FFTの性質上，音高に関わる分析をしようとすると実装や分析精度の向上に手間がかかります。

そこで，この記事では音楽信号の分析によく利用される定Q変換 (CQT: Constant-Q Transform) と呼ばれる時間周波数分析の手法の仕組みを紹介します．

なお、本記事をベースにしたPython実装の解説がありますので、もしよろしければご覧ください。

www.wizard-notes.com

はじめに
FFT / STFTでの音高分析の問題
定Q変換のアイディア
定Q変換の改良手法
参考文献・参考ページ
関連手法

FFT / STFTでの音高分析の問題

音信号の時間周波数分析でよく使われるFFT (高速フーリエ変換) ) ／STFT（短時間フーリエ変換）ですが，音高を分析することを考えると，

FFTの各中心周波数は音高の周波数と対応が取れていない
周波数分解能の問題

という２つの問題があります．

この問題を理解するために，FFTの各周波数ビンの中心周波数を眺めてみましょう。

例えば，サンプリング周波数 8 kHz，信号長 256サンプルであれば，

0, 31.25, 62.5, 93.75, 125,156.25, 187.5, 218.75, 250, ..., 4000

というように中心周波数は等間隔に並んでいます。これを図で表すと以下のようになります．

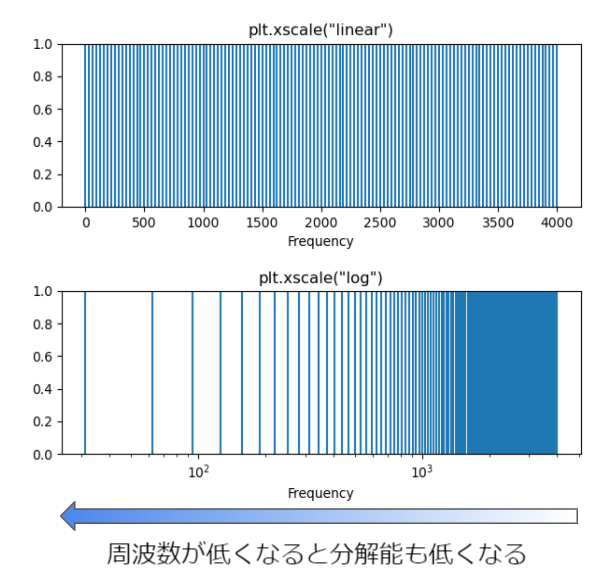
f:id:Kurene:20210709004638p:plain:w400

図の上側は水平軸を線形に，下側は対数で表しています．

一方，12音平均律（ドレミファ…）の各音高の周波数をプロットしてみます．

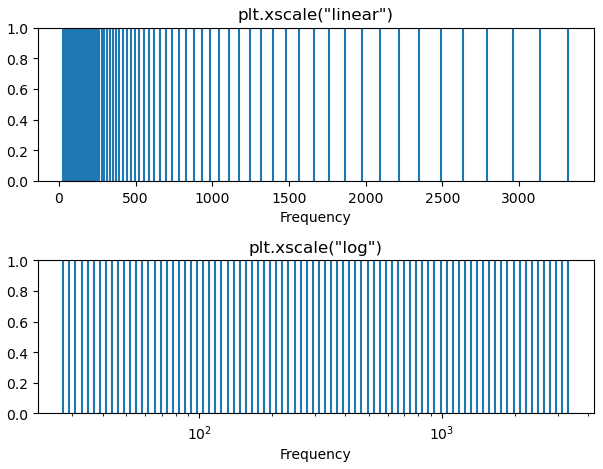
f:id:Kurene:20210709005612p:plain:w400

音高では，線形軸では高周波数になるほど音高間の間隔が広がっているのが分かります．

従って，FFTのスペクトログラムを音高の観点で見ると，

FFT周波数ビンの中心周波数と音高の周波数の対応がとれていない
低域では分解能が低く，高域では分解能が過剰に高い

という状態になっています．

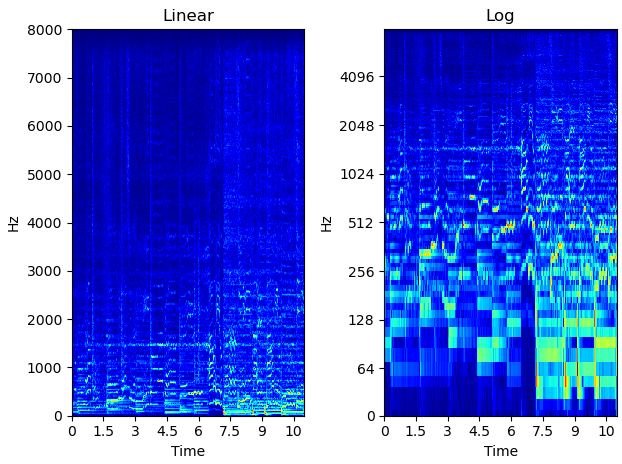
実際の楽曲のスペクトログラムでも確認することができます．

米津玄師 - Lemon サビ

f:id:Kurene:20210709010934p:plain:w500

定Q変換のアイディア

FFTで「低域では分解能が低く，高域では分解能が過剰に高い」現象はなぜ起こるのでしょうか。

「小野測器ー周波数分解能はどのように決めるのか？」によると，FFTの周波数分解能 $\Delta f$ は、

$\Delta f=\frac{f_{s}}{N}$

となっています。ここで $N$ は分析する時間窓のサンプル数です．

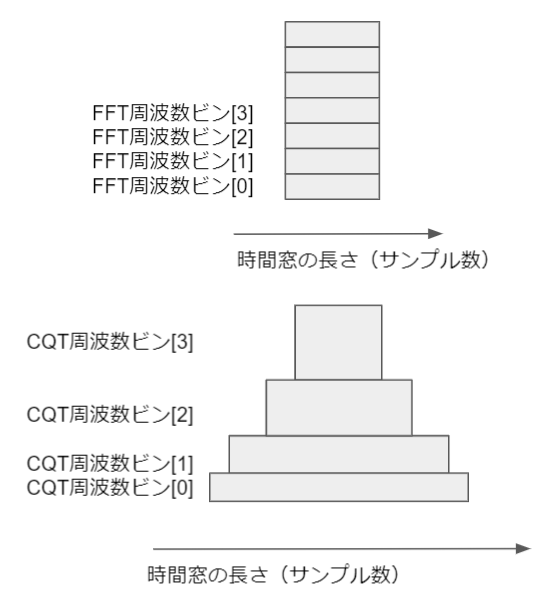
FFTは各周波数で時間窓のサンプル数（長さ）が一定であるため，全ての周波数で同じ周波数分解能となっています．

定Q変換では，中心周波数に応じて時間窓のサンプル数（長さ）を変えることで周波数分解能を等比的を変えています．

イメージとしては下の図のようになっています。

f:id:Kurene:20210709191110p:plain:w500

定Q変換の定式化

Constant-Q transform toolbox for music processing をベースに実装方法を解説します．

離散時間領域信号 $x(n)$ のCQTのスペクトル系列 $X^{CQ}(k,n)$ は以下の式で求めます。

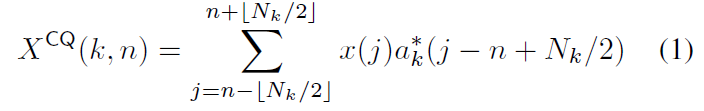
f:id:Kurene:20210710112951p:plain:w500

ここで，k = 0, 1, ... , K-1 は CQT の周波数ビン，n = 0, 1, ... , N-1 は時間フレームを表し， $\lfloor \rfloor$ は床関数による整数丸め）です．

$a^\ast_k(n)$ は $a_k(n)$ の複素共役であり，以下のように定義されます．

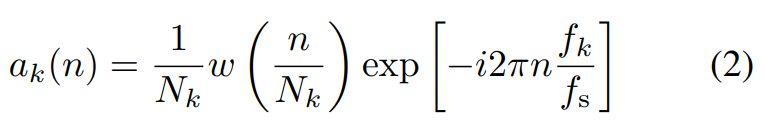
f:id:Kurene:20210710113913p:plain:w500

ここでCQT周波数ビンの窓の長さ $N_k$ は、

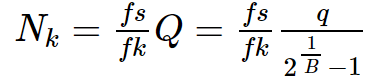
f:id:Kurene:20210710114952p:plain:w400

と定義されています．したがって，(2)の式は

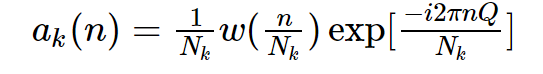
f:id:Kurene:20210710115429p:plain:w500

とも書けます。

上記のQが quality factorと呼ばれ，CQT中心周波数 $f_k$ が高いときは窓幅を小さくし， $f_k$ が低いときは窓幅を大きくして時間周波数分解能を一定に保つ働きをします．

なお，CQT の中心周波数は $f_k$ は

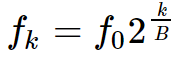
f:id:Kurene:20210710141800p:plain:w200

として等比的に決定します。

パラメタの整理

事前に決める必要があるパラメタを整理します。

B
- 1オクターブを何分割するか
- B=12 あれば12分割（12音平均律）
- 中心周波数の分割基準となる，最も小さい中心周波数
- $f_0$ と B が決まれば，CQT中心周波数[f_{k}]が算出できます
- 一般的な音楽データの音高分析であれば，[tex:f_0=440/2^m]をよく使います
  - A4=440 Hz
q (0<q≦1)
- 周波数分解能を調整するパラメタ
- q を小さくすると周波数分解能は低下するが，窓幅 $N_{k}$ が短くなり，計算量は少なくなる
- 分解能としては，q=0.5, B=48とq=1, B=24は同じになる
- 窓関数　ハン窓，ハミング窓など

スパース行列演算による高速化

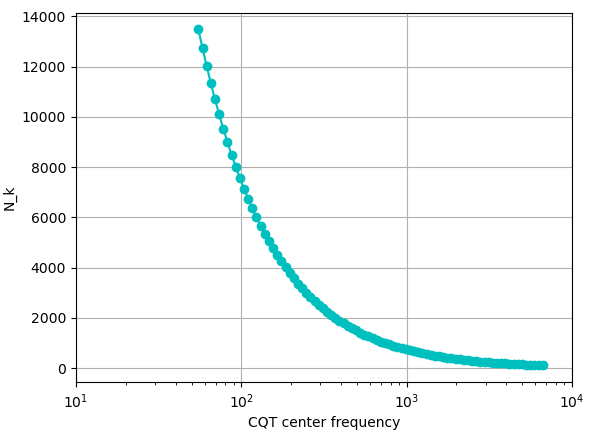
FFTの計算量は O(N log N) ですが，定Q変換を上記の式で実装すると計算量が多すぎるという問題があります。

具体的には，低域で窓幅 $N_k$ が非常に大きくなってしまいます。

f:id:Kurene:20210710143303p:plain:w500

そこで，FFTを使った式変換と疎行列を使った計算によって計算量を減らす手法が提案されています．

まず，FFTを使った式変換はパーセバル定理を使います。

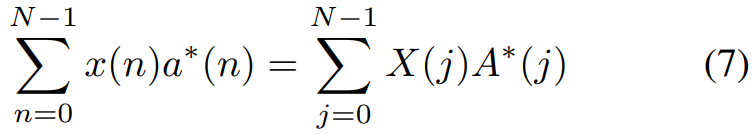
f:id:Kurene:20210710144251p:plain:w500

ここで， $X, A^\ast$ は $x, a^\ast$ をFFTした信号になります． $a^\ast$ はテンポラルカーネル， $A^\ast$ はスペクトルカーネルとも呼ばれます。

最終的にCQTのスペクトル系列は以下の式で算出できます．

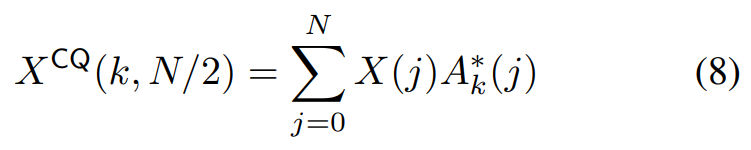
f:id:Kurene:20210710145107p:plain:w500

このスペクトルカーネル $A^\ast$ は事前に計算可能であり，非常にスパース（値がゼロの要素が多い）行列となっています．

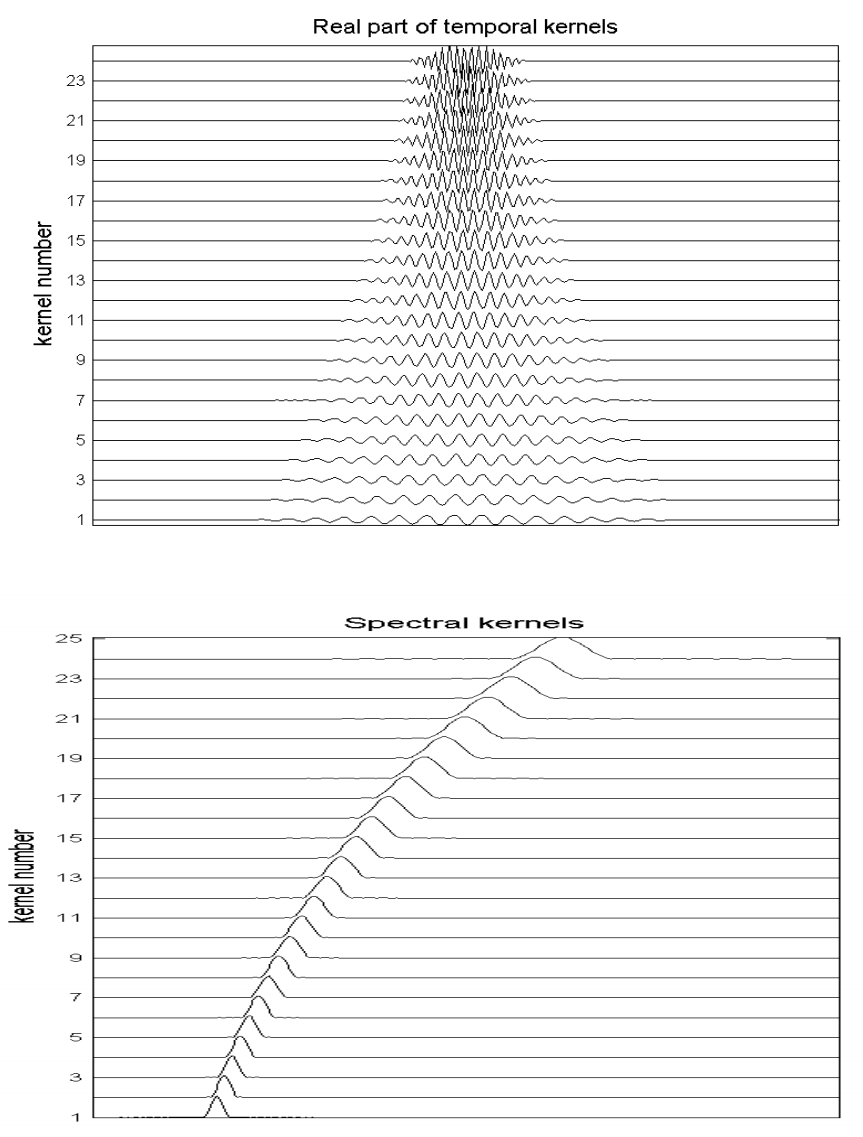
f:id:Kurene:20210710120517p:plain:w400

従って、時間フレーム単位でみると，以下の図のようにスペクトルカーネル行列と信号のFFTスペクトルベクトルの積を疎行列演算すれば効率的にCQTスペクトルを算出できます．

f:id:Kurene:20210710153626p:plain:w500

定Q変換の改良手法

スパース行列演算で計算量を削減することができましたが，さらなる改良がおこなわれています．

再帰的サブサンプリング方法
- マルチレート処理風にオクターブごとに計算することで計算効率が向上
- 実用的な逆変換を実現
- librosa.cqt , librosa.icqt はこの方式
変Ｑ変換
- 定Q変換では低域の窓幅が大きいことが問題
- Q値を線形に変化させることで窓幅が大きくなるのを緩和
- librosa.vqt

参考文献・参考ページ

Constant-Q transform - Wikipedia
GCT731 Fall 2014 Topics in Music Technology - Music Information Retrieval Audio and Music Representations (Part 2) 1.
"Calculation of a constant Q spectral transform."
- CQTの提案論文
"An efficient algorithm for the calculation of a constant Q transform". 10.1121/1.404385, 1992.
- FFTとパーセバル等式で効率化
"Constant-Q transform toolbox for music processing"
- マルチレート処理（再帰的ダウンサンプリング）実装の提案
"A Matlab Toolbox for Efficient Perfect Reconstruction Time-Frequency Transforms with Log-Frequency Resolution"
- 変Ｑ変換

Wizard Notes

Python, JavaScript を使った音楽信号分析の技術録、作曲活動に関する雑記

定Q変換 (CQT: Constant-Q Transform) の解説（音高・コード・メロディの分析向け）