※2022/9/28: λの算出式の符号が間違っていたためプロットとともに修正
信号処理におけるフィルタとしては、ローパス/ハイパスフィルタのような振幅特性を活用するフィルタが良く知られています。
しかし、一方で位相特性のみに影響を与えるオールパスフィルタという種類のフィルタがあります。
実は、オールパスフィルタは並列回路で利用することで様々な周波数特性を低演算量で実現できる非常に便利なフィルタです。
そこで本記事では、オールパスフィルタ―の概要・使い方・利用例を紹介したいと思います。
オールパスフィルタ―とは
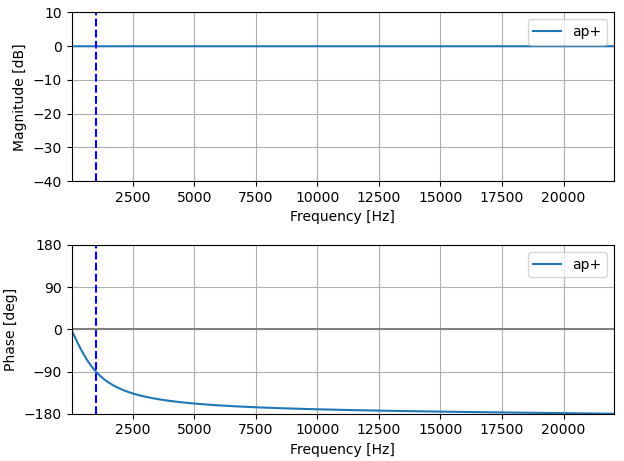
オールパスフィルタ―*1とは、入力信号の振幅特性を変えず*2に位相特性のみを変化させるフィルタです。
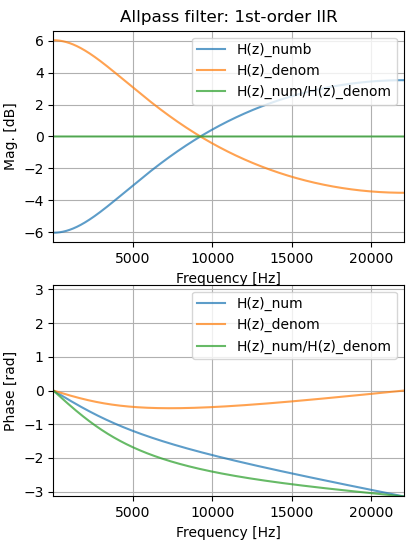
例えば、以下は1次オールパスフィルタの周波数特性です。
どんな利用用途があるか?
オールパスフィルタどうしを直列接続した場合、回路全体もオールパスフィルタとなるため、出力信号は位相特性のみ変化します。
オールパスフィルタの直列接続はあまり利用されませんが、距離に相当する時間遅延の付与や、振幅特性を保ったまま時間波形の形状・幅を変化させることができます。
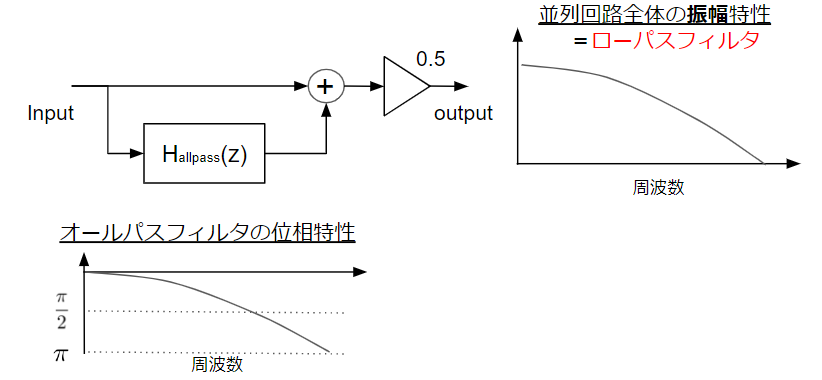
一方で、オールパスフィルタは並列接続で絶大なる効果を発揮します。
[ px]
px]
上図のようなオールパスフィルタを使った並列回路はローパスフィルタとして動きます。
具体的には、1次IIRオールパスフィルタの出力は入力信号に対して
- 低周波: 位相はほぼ変わらない
- 高周波: 位相は180度遅れる
といった位相特性を持つため、高周波では入力信号の逆位相信号となっています。
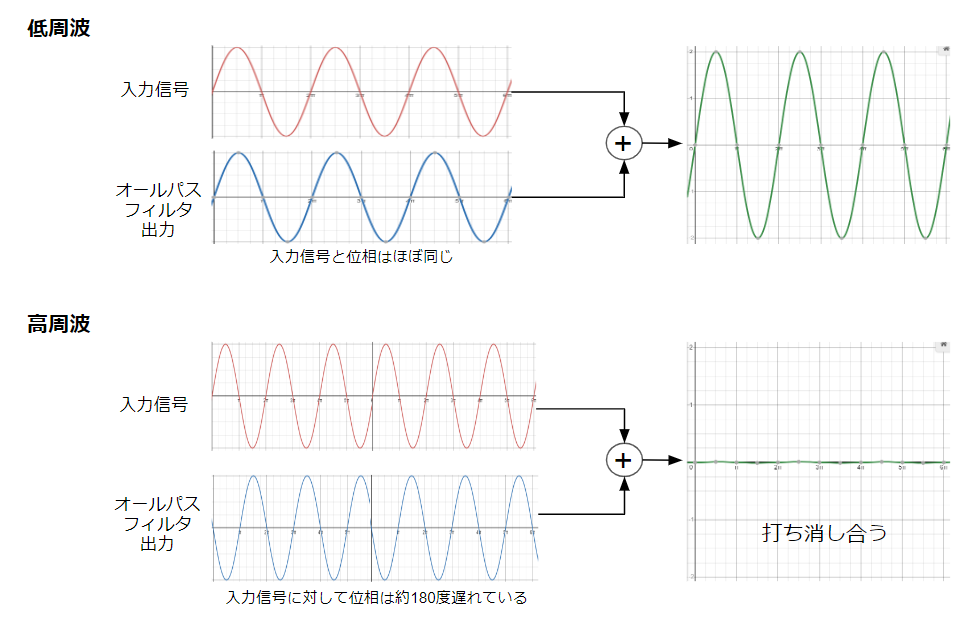
従って、入力信号とオールパスフィルタ出力信号を足すと高周波では打ち消し合うため低周波の成分だけ残ります。
[ px]
px]
これはローパスフィルタの特性そのものです。
まとめると、並列回路では、入力信号の特定の周波数帯域の位相を変化させた中間信号を作成し、その中間信号と入力信号の加算によって並列回路全体としては所望の周波数帯域だけを強調したり除去したりすることができます。
つまり、オールパスフィルタさえあれば様々な周波数特性のフィルタを作ることができます。
オールパスフィルタのフィルタ構成
単純な遅延 (FIRフィルタ)
最も簡単な例は、単に遅延を与えるだけです。
これは直感的に分かるように、信号がDサンプル遅れます。
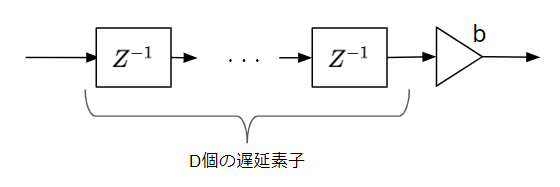
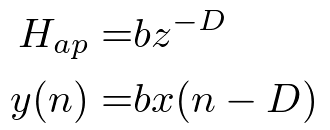
ここで、b=1.0もしくはb=-1.0であれば振幅特性は全く変化しません。
もしb=0.5、b=-0.5のような場合、信号のゲインは変わりますが振幅特性としては全周波数で同じゲイン (=フラット)です。
注目すべきは bの符号であり、負の場合は位相が反転するので出力信号は正の場合と比べると逆位相となります*3。
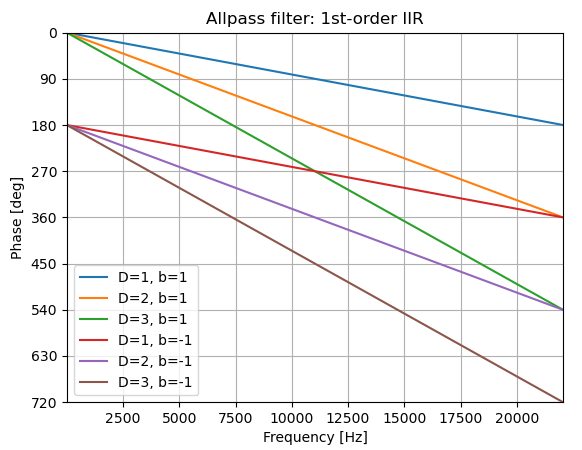
以下は、D変えた時のb=1.0とb=-1の位相特性です。
出力信号は遅延素子1個につき最大で180度位相が遅れます。
ただし、それはナイキスト周波数付近の話であり、低周波の位相を変化させるためには多くの遅延素子が必要です。
最後に、単純な遅延素子によるオールパスフィルタの並列回路を考えてみます。
これは普段扱っているFIRフィルタに他なりません。
このことはディジタル信号処理において位相に着目して設計することの重要性を表しています。
1次IIRオールパスフィルタ
先ほどの単純な遅延の場合、位相特性は線形でした。そのため、低周波の位相を変化させるためには多くの遅延素子で必要となります。
それを解決する手段である1次IIRオールパスフィルタは非線形な位相特性を持つことができます。
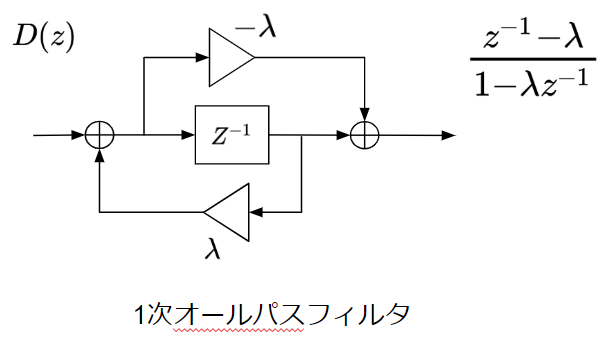
1次オールパスフィルタでは、単純な遅延素子1個の場合と同じく位相を最大で180度遅らせることができます。
さらに係数λ(-1<λ<1)を変更することで、各周波数における位相の変化度合いを制御することができます。
伝達関数より、λ=0の場合は単純な遅延素子1個と等価になります。すなわち、単純な遅延によるオールパスフィルタは1次IIRオールパスフィルタの特殊な例となります。
このλ=0の場合において、サンプリング周波数の4分の1の周波数で位相が90度遅れます。これを基準として1次IIRオールパスフィルタの特性を観察します。
b = np.array([-lam, 1.0]) a = np.array([1.0, -lam])
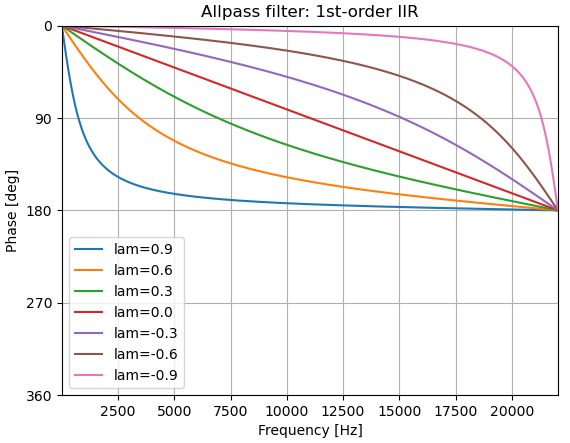
λが正の場合は単純な遅延素子1個よりも低周波で位相が遅れます。
一方、λが負の場合は低周波で位相の遅れが少なくなります。
従って、1次IIRフィルタではλを制御することで各周波数の位相の遅れ具合を制御することができます。
このλの決定方法ですが、以下の式が知られています。
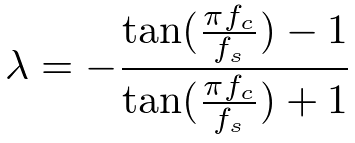
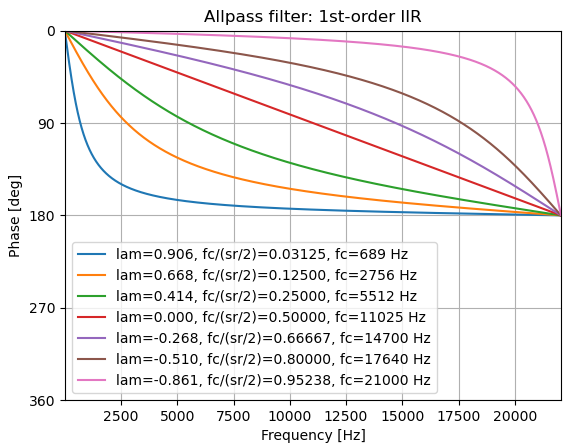
上記の式により、位相が90度遅れる周波数をfcとして1次IIRオールパスフィルタの係数λを決定することができます。
lam = -(np.tan(np.pi*fc/sr)-1)/(np.tan(np.pi*fc/sr)+1) b = np.array([-lam, 1.0]) a = np.array([1.0, -lam])
2次IIRオールパスフィルタ
双2次フィルタとしてエフェクタ等でよく利用されるのが2次IIRオールパスフィルタです。
フィルタの形式は1次IIRの直列接続として考えることができます。
b = np.array([lam1*lam2, -(lam1+lam2), 1.0]) a = np.array([1.0, -(lam1+lam2), lam1*lam2])
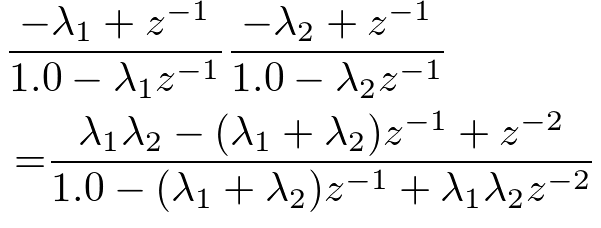
このように、2つのパラメタ λ1 , λ2を制御することで位相を変化させることができます。
基本的には、1次IIRの位相が90度遅れる周波数よりλ1 , λ2を算出することになります。
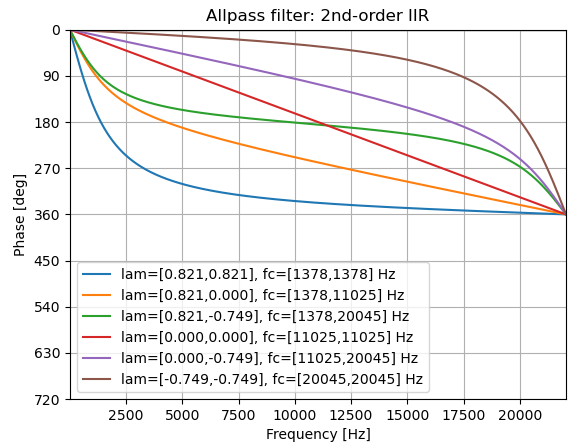
しかし、2つのフィルタの位相遅延が加算されるため、結果的には fc1, fc2で位相がどのくらい遅れるかを制御するのは困難です。
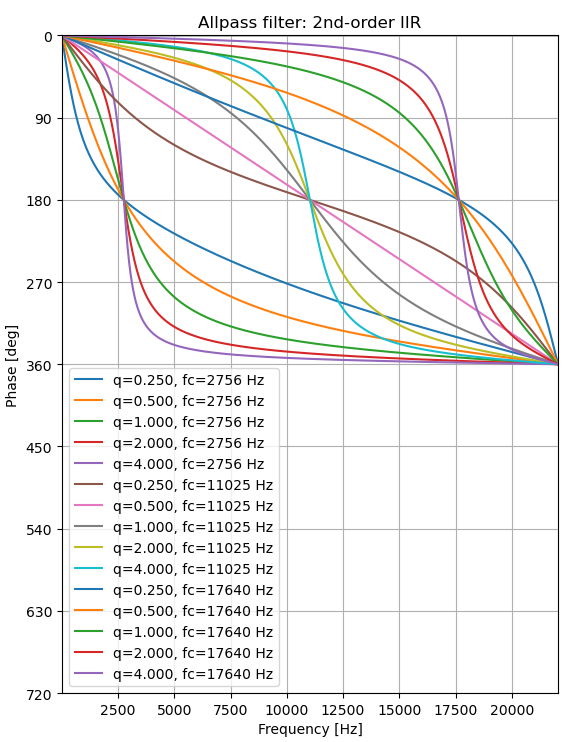
一方で、より制御しやすい形式として、Audio EQ Cookbookのような係数の設定方法が知られています。
この方法では、180度位相が遅れる周波数 fc と、フィルタのQ値(どのくらい急峻に特性を変化させるか)q を設定することで位相特性を制御できます。
w = 2.0 * np.pi * fc / sr cos_w, sin_w = np.cos(w), np.sin(w) alpha = 0.5 * sin_w / q b = np.array([ 1.0 - alpha, -2.0 * cos_w, 1.0 + alpha, ]) a = np.array([ 1.0 + alpha, -2.0 * cos_w, 1.0 - alpha, ])
N次IIRオールパスフィルタ
N次オールパスフィルタを設計する方法は2つあります。
1つは2次IIRフィルタのようにN個の1次IIRフィルタを直列接続する方法です。
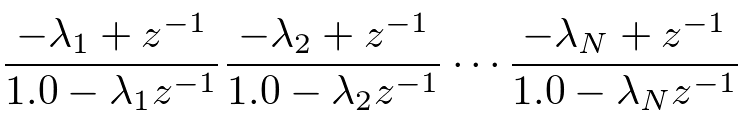
もう1つは、分母項と分子項で対称的な係数を持つ必要があります。1次IIRフィルタを直列接続はこれを満たします。
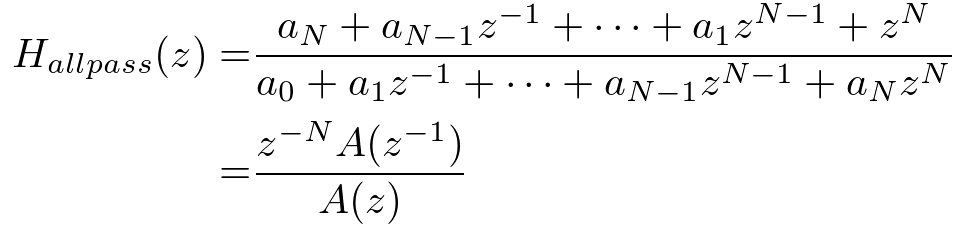
これは複素単位円上で考えると、極と零点は同じ角度にありますが、複素単位円を境界に大きさが逆となっています。
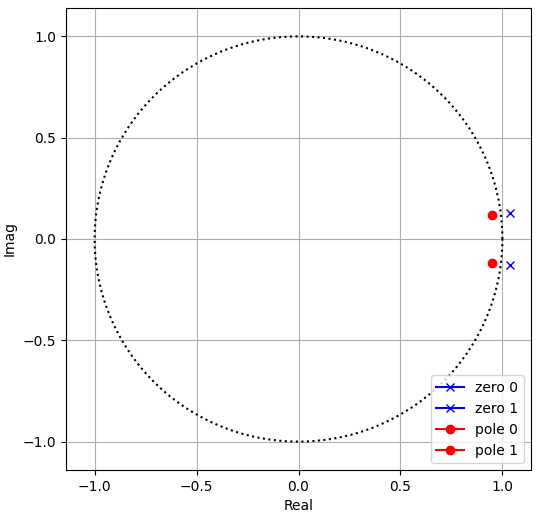
すなわち、分子項のFIRフィルタと分母項のIIRフィルタの直列接続として、振幅特性は加算された結果として打ち消しあい、位相特性では両方の位相遅れが加算されます。
オールパスフィルタのメリット
では、なぜオールパスフィルタを使って並列回路でフィルタを構成するのでしょうか。
それには以下のようなメリットがあります。
- フィルタ係数をより少数のパラメタで表現できる
- 情報圧縮的な観点
- 演算量の削減
- フィルタが安定している
- 不安定なフィルタを安定なフィルタに変換する際に利用されます
- 伝送等でオールパスフィルタの係数に雑音が混ざってもフィルタは安定*4
オールパスフィルタの応用例
様々な特性のフィルタを構成
より少ない次数でIIRフィルタを構成
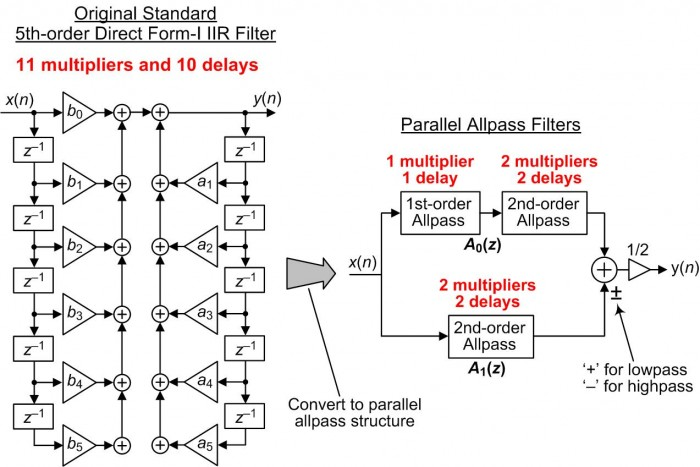
フィルタの周波数特性の伸縮
マルチバンドオーディオクロスオーバーフィルタ処理
www.wizard-notes.com www.wizard-notes.com
適応ノッチフィルタによる周期性雑音の除去/強調
オーディオエフェクタとしての利用(フェイザー)
執筆予定
まとめ
様々な周波数特性を実現するオールパスフィルタ―の概要、使い方、利用例を紹介しました。