音響信号処理の良い参考書であるプログラム101付き音声信号処理では、適応信号処理の一例として適応ノッチフィルタが紹介されています。

ただし、プログラムがC言語のみであり、また、数学的な説明が僅かであるため仕組みが分かりにくいです。

そこで、適応ノッチフィルタのPythonにおけるリアルタイム実装とアルゴリズムの詳細を説明したいと思います。

適応ノッチフィルタについて

信号処理における雑音除去の一つのユースケースについて、未知の狭帯域雑音（正弦波信号）を除去が挙げられます。

具体的な対象としては、交流電源由来のノイズやモーター／エンジンなどの回転音、音楽信号であれば調波楽器の基音・倍音成分です。

これらの周期性の信号は予め周波数が既知であれば固定のノッチフィルタでよいのですが、状況／環境によって除去したい正弦波の周波数が揺らいだり変化することが考えられます。

そこで、除去したい正弦波の周波数の変化に追従するために適応ノッチフィルタが利用されます。

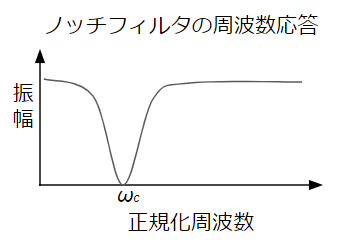
適応ノッチフィルタの仕組み

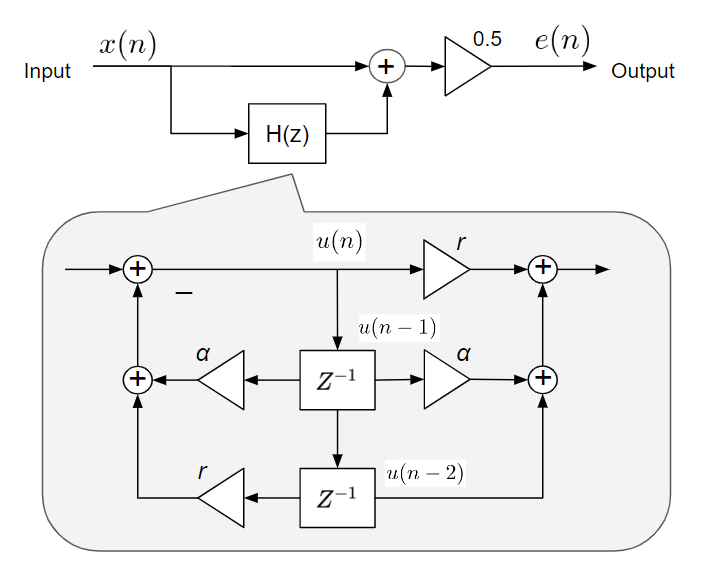
よく利用される適応ノッチフィルタは2次IIRで構成されるオールパスフィルタを利用しています。

回路全体としては、このオールパスフィルタと未処理の信号の並列回路となっています。

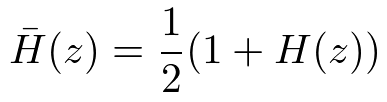
このオールパスフィルタの形状は以下のようになっています。

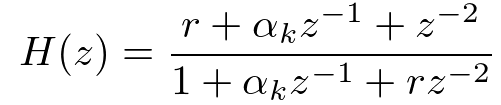
rがノッチフィルタの幅を決めるパラメタです。また、αがノッチフィルタの中心周波数に紐づくパラメタであり、以下のような関係性があります。

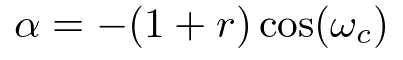
従って、適応ノッチフィルタでは周波数が未知の正弦波が除去できるようにノッチフィルタの中心周波数 ωcを逐次推定します。

問題設定として、所望信号である広帯域信号の中に混ざっている狭帯域信号（除去したい正弦波信号）のパワーは大きいと仮定します。

その場合、最適化方針としては適応ノッチフィルタ適用後の出力信号のパワーが最小になればＯＫです。

従って、以下の出力信号 e(n) のパワーの時間平均 E[e²(n)] をαについて最小化します。

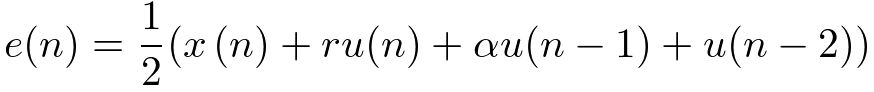
最終的に、E[e²(n)]をαで微分してNLMSアルゴリズムを適用すると以下の更新式を導出することができます。

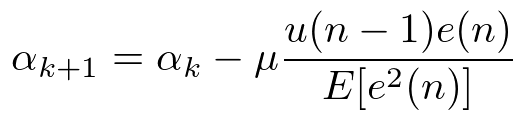
ここで、u(n-1)e(n)は中間信号と出力信号の瞬時値、E[e²(n)]は出力信号パワーの時間平均、μはステップサイズになります。

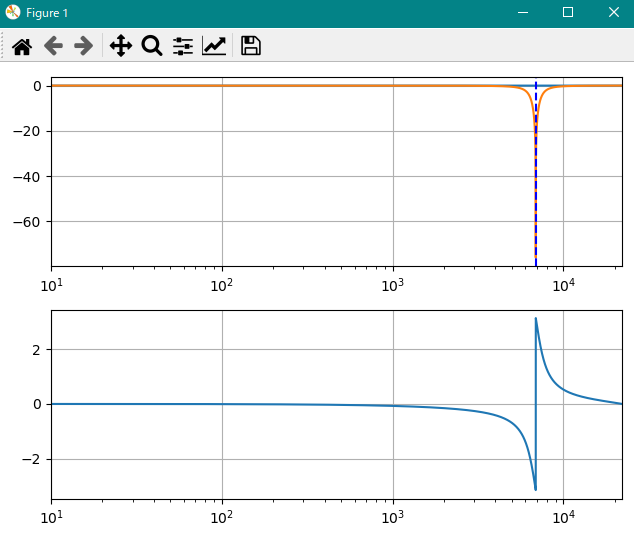
α=1.0, r=0.9とした時のフィルタの周波数特性をプロットしました。

点線はαから算出したノッチフィルタの中心周波数であり、振幅が急激に小さくなることが分かります。

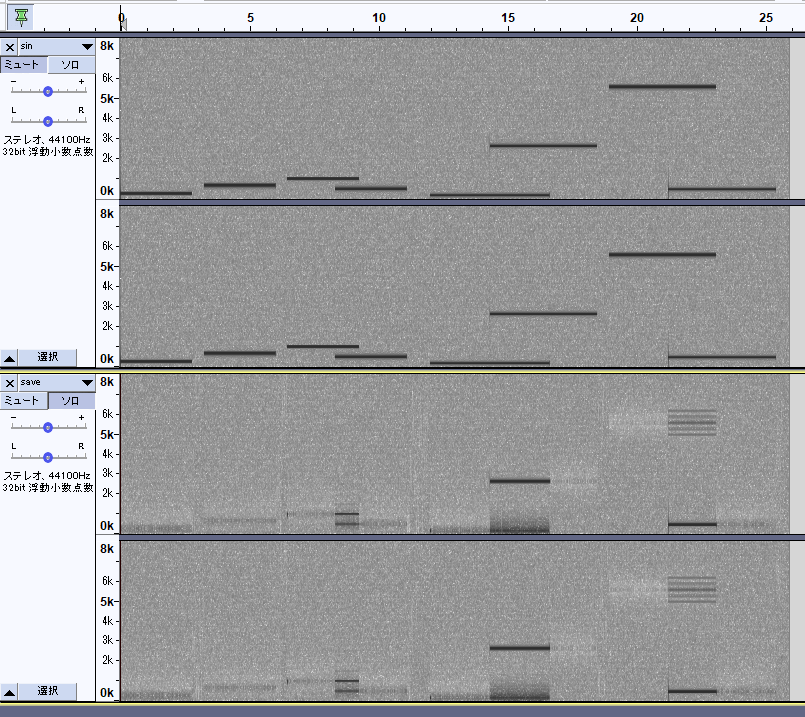
上図が白色雑音＋適当なサイン波を混ぜた入力信号であり、下図が適応ノッチフィルタの出力信号です。

正弦波が一つだけ出現している区間では、正弦波を抑圧できていることが確認できます。

ただし、正弦波が複数なっている区間では１つの正弦波しか抑圧できていません。

従って、複数の正弦波を抑圧するためには複数の適応ノッチフィルタが必要となります。

実際に音として聞いてみると、上手く消えている区間ではサイン波の鳴り始めは一瞬聞こえるもののすぐに消音されていることが分かります。

プログラム101付き音声信号処理を参考に，適応ノッチフィルタのPythonにおけるリアルタイム実装とアルゴリズムの詳細を説明しました。

次回は、複数の適応ノッチフィルタを適用した例を紹介したいと思います。