リアルタイム声質加工プラグインの開発進捗。
— Kurene (@_kurene) July 18, 2020
声を太くしたり子供っぽくしたりできる処理のデモです。 pic.twitter.com/JcfwPJ2OCc
線形予測分析+周波数ワープでリアルタイムで声質を加工する処理を作りました。
ボイスチェンジャー関連の処理は興味を持っている方が多いと思いますが、Web上に情報が少ないのが現状だと思います。
そこで、走り書きになりますが、私が作ったデモにおける声質加工フィルタの設計・実装方法を書き残したいと思います。お役に立てれば幸いです。
Step 1. 声道共振成分の抽出
まず、線形予測分析やケプストラム分析を使って、声道特性(声道の共振特性)を表現するフィルタ係数を抽出します。
上記の線形予測分析の例のように、音声信号から抽出した声道共振特性を表すフィルタ係数は、FIRフィルタとして使えば声帯音源信号の抽出に、IIRフィルタとして声帯音源信号に適用すれば音声信号を合成することができます。
このフィルタの係数を加工することで、元の音高を保ったまま声質を変化させたり元の音素を別の音素に近づけることができます。
その一例として、デモのようにフィルタの周波数振幅応答を伸縮すると、声質を太くしたり子供っぽくすることができます。
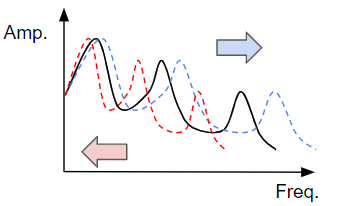
今回は、このようなフィルタの作成を考えてみます。
Step. 2 周波数ワープ
声道共振特性を抽出するK次のFIRフィルタ係数が抽出できているとします。
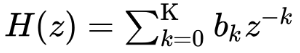
このK+1個の係数をフィルタの周波数振幅応答が伸縮するように修正し、逆フィルタを声帯音源信号に適用することで声道共振特性を変化させます。
しかし、Kが大きい場合、K+1個もの係数を全部調整して所望の周波数振幅応答を得るのは効率的ではありません。
今回はスペクトル包絡の伸縮なので、1つのパラメタでスペクトル包絡を伸ばしたり縮ませたりすることができれば便利ですね。
そこで、周波数ワープ(伝達関数の変数変換)を使います。
この方法は、ディジタルフィルタの遅延要素を一次オール-パス・フィルタに置き換えることで、フィルタの周波数振幅応答を非線形に変形することができます。
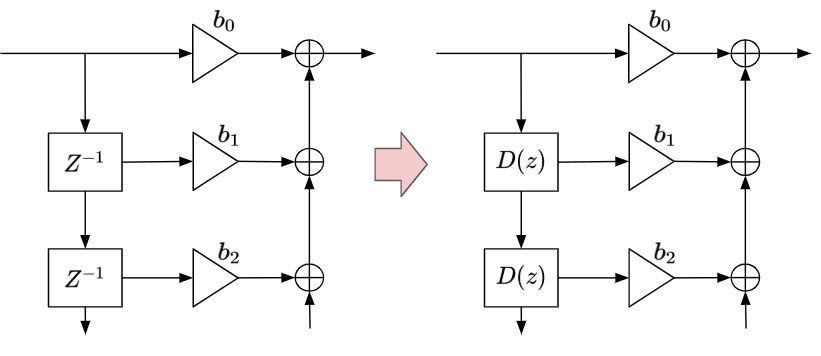
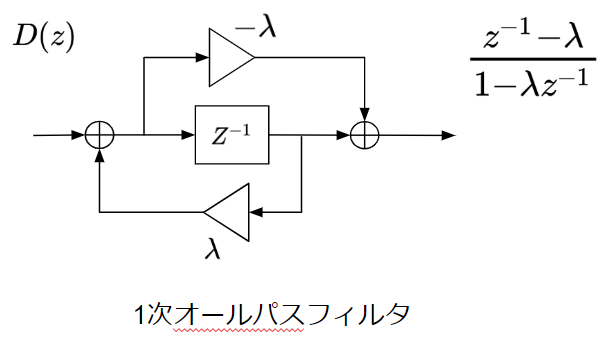
Warped LPC などでは、周波数特性をバーク尺度やメル尺度のような人間の聴感特性に合わせて変形させることを目的に利用されています。
具体的なパラメタとしては、上記の1次オールパスフィルタの係数λ (-1<λ<1) を変更することで、フィルタの周波数振幅応答を伸縮させることができます。
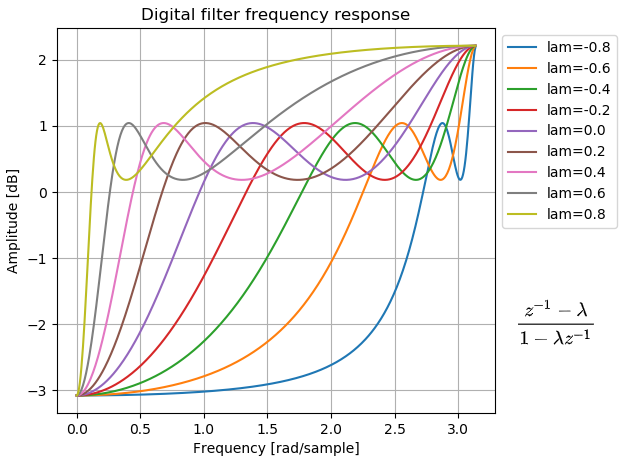
Step 3. 声道共振特性を変形させたフィルタの実装方法
今回は、声道共振特性の逆フィルタであるFIRフィルタを変形してみました。
以下のように最終的にIIRフィルタの形式で表すことができれば、IIRフィルタとして実装すればOKと考え、係数を展開・整理します。
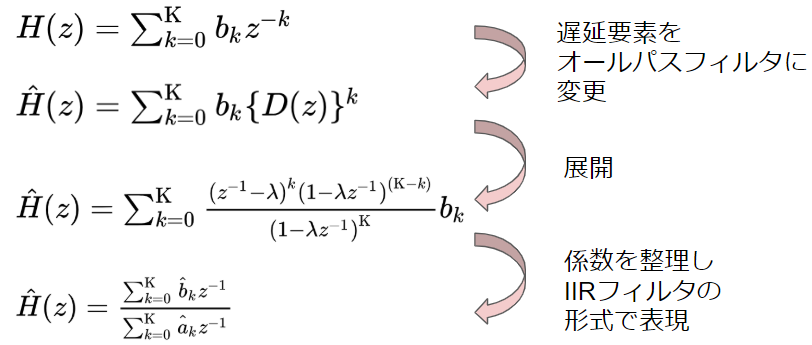
3番目の式をもう少し整理してみます。
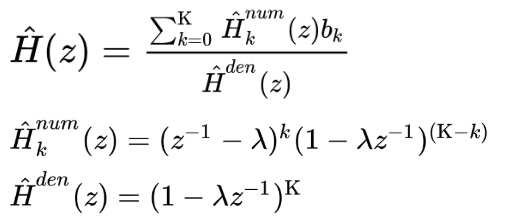
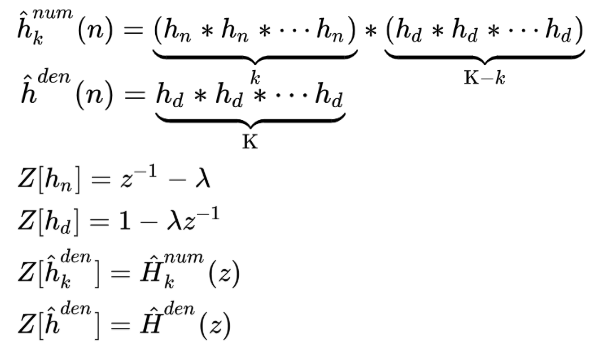
結局のところ、 も
も1次オールパスフィルタの分子または分母のフィルタ係数系列をK回畳み込むことで算出することができました。
最終的に声帯音源信号に対して逆フィルタ をフィルタリングすることで、加工した声道共振特性を付与することができます。*1
演算量に関する考察
声道共振特性の場合、10~20ミリ秒程度の時間フレームごとにフィルタを求めることになります。そのため、
時間フレームごとに毎回を一から算出するのは、それなりに演算量が大きくなるので避けたいところです。
ここで、先ほどの式をもう一度見てみます。
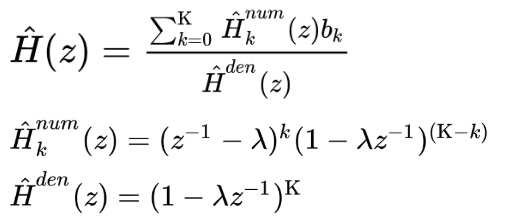
実は、も
も1次オールパスフィルタの変数 λ にのみ依存しています。
つまり、どちらも声道共振特性フィルタの係数には依存していないため、例えば1次オールパスフィルタの変数 λ が固定の場合は事前に計算しておくことができます。
また、λが変化する場合でも、
- 次にλが変化するまでは、同じ
を使い続ける。また、一度計算したらメモリに保持しておく
- λの取りうる値を制限し、各λの値に対応する
を計算してテーブルとして持っておく
のような工夫をすることで演算量を減らすことができます。
参考文献
- 越田 俊介, 阿部 正英, 川又 政征, "可変ディジタルフィルタ"
- Härmä, Aki, et al. "Frequency-warped signal processing for audio applications." Journal of the audio engineering society 48.11 (2000): 1011-1031.