逆関数法で一様分布・指数分布と算出（Python実装）

ゲームやCGの実装をしていると,「いい感じに偏った乱数が欲しい」と思うことが多々あります*1。

よく知られている方法として、rand関数などで算出した一様乱数を元に逆関数法で乱数を作ることができます。

ただ、数式の意味が分かりにくいところもあります。

そこで、備忘録として逆関数法を理解をまとめ、また、Pythonで実装してみました。

逆関数法の理解

逆関数法の説明は、以下の資料が分かりやすいです。

Rで学ぶ逆変換（逆関数）法 from Nagi Teramo

C言語による乱数生成

ただし、いきなり○○分布の累積密度関数の逆関数から考えると分かりにくい気がします。

結局のところ、図のように [0.0, 1.0) の一様乱数を、どのように偏りをもたせて写像するかということだと思います。逆関数の傾きが緩やかな区間では、その区間に対応する x の出現確率は高くなります。

その際、よく知られた分布（e.g. 指数分布）を得るには、その分布の累積密度関数の逆関数を使えばOKです。

コンプレッサーやディストーション、FMシンセの信号処理のように、入力をどう歪ませて出力するかという設計に似ていますね。

例

一様分布[0, 1) => 一様分布[0, 1)

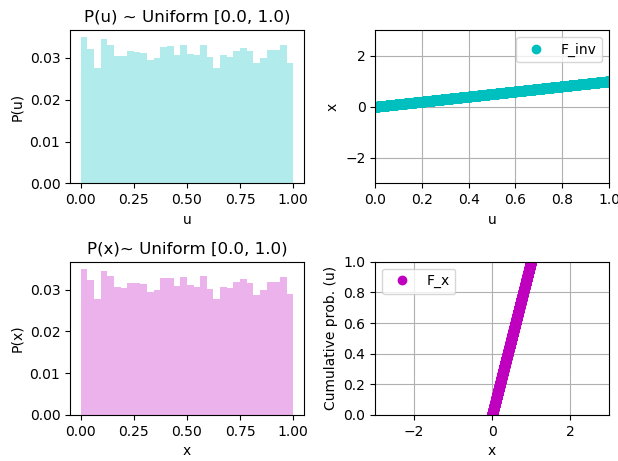
累積密度関数の逆関数は F_inv(u)=u となります。

一様分布[0, 1) => 一様分布[0, 3.0)

累積密度関数の逆関数は F_inv(u)=3.0 * u となります。

一様分布[0, 1) => 一様分布[-1.0, 1.0)

一様分布[0, 1) => 指数分布 (λ=2.0)

#

一様分布[0, 1) => 指数分布 (λ=5.0)

まとめ

逆関数法による任意の確率分布に従う乱数生成は、初見だと分かりにくいですが、[0,1) の一様乱数を任意の区間の一様乱数に変換することから考えると、よくプログラミング入門で取り組む、rand関数の区間調整の式の逆関数が出てくるので分かりやすいと思いました。

スクリプト

import numpy as np
import matplotlib.pyplot as plt


def plot_dist(u, F_x, F_inv, label):
    x = F_inv(u)
    x_sorted = np.sort(x)
    u_sorted = np.sort(u)
    
    plt.clf()

    plt.subplot(2,2,1)
    weights = np.ones(len(x))/float(len(x))
    plt.hist(u, bins=32, color="c", alpha=0.3, weights=weights)
    plt.xlabel("u")
    plt.ylabel("P(u)")
    plt.title("P(u) ~ Uniform [0.0, 1.0)")

    plt.subplot(2,2,3)
    weights = np.ones(len(x))/float(len(x))
    plt.hist(x, bins=32, color="m", alpha=0.3, weights=weights)
    plt.xlabel("x")
    plt.ylabel("P(x)")
    plt.title(f"P(x)~ {label}")
        
    plt.subplot(2,2,2)
    plt.plot(u_sorted, F_inv(u_sorted), "bo", c="c", label="F_inv")
    plt.grid()
    plt.xlim(0.0, 1.0)
    plt.ylim(-3.0, 3.0)
    plt.xlabel("u")
    plt.ylabel("x")
    plt.legend()
    
    plt.subplot(2,2,4)
    plt.plot(x_sorted, F_x(x_sorted), "bo", c="m", label="F_x")
    plt.grid()
    plt.ylim(0.0, 1.0)
    plt.xlim(-3.0, 3.0)
    plt.ylabel("Cumulative prob. (u)")
    plt.xlabel("x")
    plt.legend() 

    plt.tight_layout()
    plt.show()


N = 10000
np.random.seed(0)
u = np.random.random(N)


label = f"Uniform [0.0, 1.0)"
F_x   = lambda x: x
F_inv = lambda u: u
plot_dist(u, F_x, F_inv, label)

label = f"Uniform [0.0, 3.0)"
F_x   = lambda x: (1.0/3.0) * x
F_inv = lambda u: 3.0 * u
plot_dist(u, F_x, F_inv, label)

label = f"Uniform [-1.0, 1.0)"
x_max, x_min = 1.0, -1.0
F_x   = lambda x:  (x - x_min) / (x_max - x_min)
F_inv = lambda u: (x_max - x_min) * u + x_min
plot_dist(u, F_x, F_inv, label)


lam = 2.0
label = f"Exp. dist. lam={lam:0.1f}"
F_x   = lambda x: 1.0 - np.exp(-lam * x)
F_inv = lambda u: -(1.0/lam)*np.log(1.0 - u)
plot_dist(u, F_x, F_inv, label)

lam = 5.0
label = f"Exp. dist. lam={lam:0.1f}"
F_x   = lambda x: 1.0 - np.exp(-lam * x)
F_inv = lambda u: -(1.0/lam)*np.log(1.0 - u)
plot_dist(u, F_x, F_inv, label)

*1:アイテムガチャとか判定とか