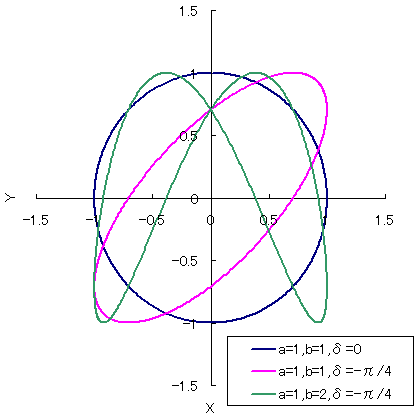DTMなどで音の広がり感を可視化するには，リサージュ図形に基づく方法があります．

リサージュリサジュー:Lissajousとは | 偏ったDTM用語辞典 - DTM / MIDI 用語の意味・解説 | g200kg Music & Software

2つの信号を元に作られるリサージュ図形を利用し，2次元平面上にプロットした点群の形状を見ることで音の広がり感を確認することができます．

例えば，iZotopeの無料プラグインである Ozone Imager V2 でも "Lissajous" をクリックすると確認できます．

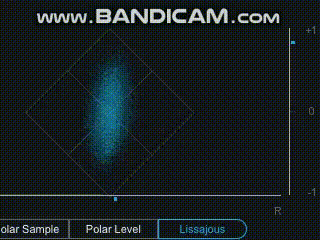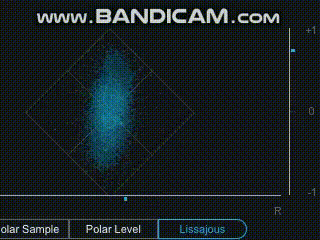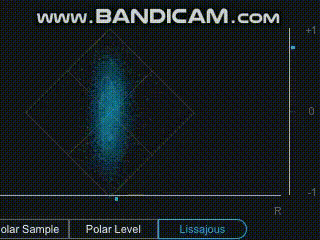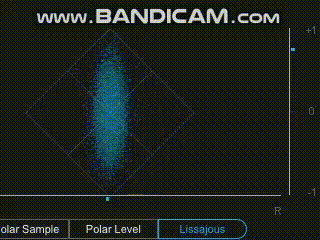
f:id:Kurene:20210619000804g:plain — Ozone Imager V2

なお，この方法により音の広がりを確認するプラグイン・機能は，

フェイズメーター
フェイズスコープ
リサージュメーター
リサジュー
ゴニオメーター
…

などと呼ばれています．

この記事ではリサージュメーターを実装し，簡単な信号で動作テストします．

実装解説
- リサジュー図形
ステレオ信号への適用
サンプルコード
- リサージュ図形
- ステレオ信号向けスクリプト
動作テスト

実装解説

リサジュー図形

f:id:Kurene:20210619100908p:plain:w300 — wikipedia - リサジュー図形

リサージュ図形は以下の式で描画することができます．

$x=A\sin (at+\delta), y=B\sin (bt)$

$A, B$ が各サイン波の振幅， $a,b$ が振動数（周波数）， $\delta$ が位相差であり，この5つのパラメタを変えるだけで多様な幾何学図形を描くことができます．

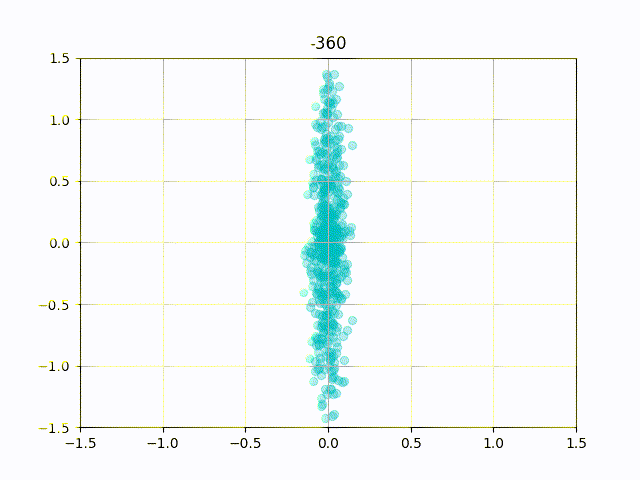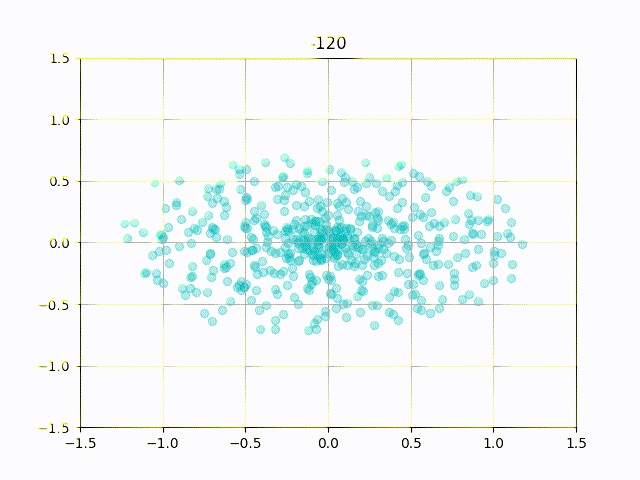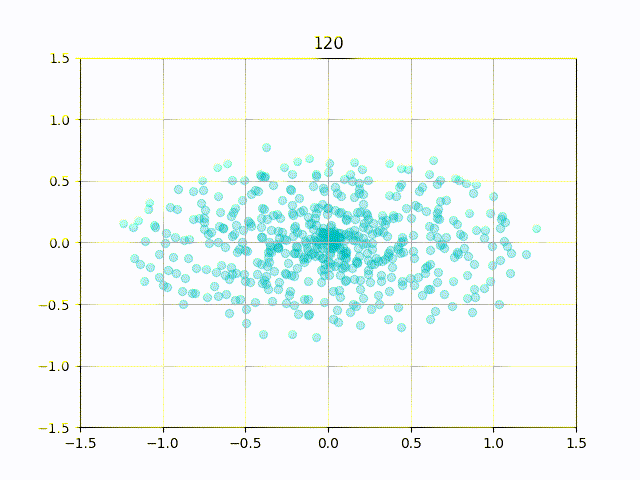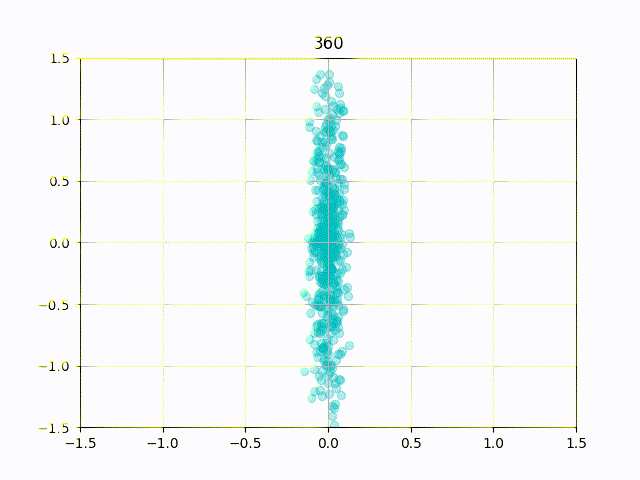
特に上記の式において $a=b=1, A=B$ と設定した場合，リサージュ図形は楕円となり，位相差 $\delta$ に応じて楕円の向きと長径・短径が変化します．

$x=A\sin (t+\delta), y=A\sin (t)$

f:id:Kurene:20210619224829p:plain:w500

具体的には，リサージュ図形の形上は

$\delta=0$ => $y=x$
$\delta=180$ => $y=-x$
$\delta=90, 270$ => [tex:x²+y²=1]

となります．

リサージュメーターではこの性質を使って，ステレオ信号の音の広がりを可視化しています．

ただし，ステレオ信号に適用する際は振幅の大きさ等の影響で，楕円領域に散らばる点群として描画されます．

ステレオ信号への適用

ステレオ信号をsig_LRとして説明します．なお，sig_LR.shape==(2, length)とし，sig_LR[0]がLチャネル信号，sig_LR[1]がRチャネル信号とします．また，lengthはフレームサイズです．

リサージュメーターとしてステレオ信号を可視化するには，L，Rチャネルのそれぞれの信号を単純にリサージュ図形のx, yとして入力します．

x = sig_LR[0,:]
y = sig_LR[1,:]

このままだと位相差0度の時に描画される図形は $y=x$ ですが，より直感的な描画にするため $x=0$ （中央）で位相差0度となるように調整します．

具体的には，以下の回転行列を使って45度回転させます．

x_mod = x / np.sqrt(2) - y / np.sqrt(2)
y_mod = x / np.sqrt(2) + y / np.sqrt(2)

x_mod，y_modを得る計算はMS処理となっており，すなわちMS信号をプロットすることでリサージュメーターを実現できます．

サンプルコード

リサージュ図形

# -*- coding: utf-8 -*-
import sys
import numpy as np
import matplotlib.pyplot as plt


def lissajous(length, deg):
    offset = np.pi *  deg / 180
    t = np.linspace(0, 1.0, length)
    x = np.sin(2*np.pi*t)
    y = np.sin(2*np.pi*t + offset)
    
    return x, y
    
    
length = 1024
deg_delta = 30
lst = range(-90, 360 +deg_delta, deg_delta)

n_samples = len(lst)
n_col     = 4
n_row     = (n_samples) // n_col
plt.clf()
for k, deg in enumerate(lst):
    print(n_row, n_col, k+1)
    plt.subplot(n_row, n_col, k+1)
    x, y = lissajous(length, deg)
    plt.scatter(x, y, s=1, c="c", alpha=0.3)
    plt.xlim([-1.5, 1.5])
    plt.ylim([-1.5, 1.5])
    plt.title(f"{deg}")
    plt.grid()
     
plt.tight_layout()
plt.show()

ステレオ信号向けスクリプト

# -*- coding: utf-8 -*-
import sys
import numpy as np
import matplotlib.pyplot as plt


sr     = 44100
length = 512 
deg    = 0

def make_sig(length, deg, bias=0.0, fo=440):
    offset = np.pi *  deg/ 180
    t      = np.linspace(0, 1.0, length)
    z      = 1.0#np.linspace(1.0, 0.0, length)
    x = np.c_[
        np.sin(2*np.pi*fo*t) * z          + bias*np.random.normal(0.0, 0.1, length),
        np.sin(2*np.pi*fo*t + offset) * z + bias*np.random.normal(0.0, 0.1, length)
        ].T

    return x


def lissajous(index, sig_LR):
    x = sig_LR[0]
    y = sig_LR[1] #/ ss
    
    xx = x/np.sqrt(2) - y/np.sqrt(2)
    yy = x/np.sqrt(2) + y/np.sqrt(2)
    
    plt.clf()
    plt.scatter(xx, yy, c="c", alpha=0.3)
    plt.xlim([-1.5, 1.5])
    plt.ylim([-1.5, 1.5])
    plt.title(f"{deg:03}")
    plt.grid()
    plt.savefig(f"r{index:03}.png")
    #plt.show()


for k, deg in enumerate(np.arange(-360, 375, 30)):
    sig_LR = make_sig(length, deg, bias=0.0)
    lissajous(k, sig_LR)