はじめに
音楽の分析では、メロディー、ハーモニー、リズムの3つ要素から特徴を捉えるのが重要です。
特にハーモニーに関しては、音楽理論による体系化(例:コード、コード進行)が出来ています。そのため、 分析した結果の意味付けがしやすいので、計算機での分析も比較的取り組みやすいと思います。
また、歌声抽出などのメロディーを抽出する技術が進歩している*1ことから、今後、メロディーの分析(例えばスケール)もホットトピックになるかもしれません。
計算機でメロディーとハーモニーの音楽的分析を行うには、楽曲から音高情報を抽出する必要があります*2。 この記事では、メロディー、ハーモニーの分析に使われる音高情報の算出方法について、自身の実装やPython(LibROSA)のコードとともに紹介します。実装と理解の助けになれば幸いです
音高 ・クロマ特徴の算出方法
処理の流れ
主に以下の2段階の処理となります(リアルタイム処理の場合は各時間ごとに各表現の列ベクトルを求めることになります)。
- 音高 ― 時間表現を算出
- ピッチクラス(音名)― 時間表現(クロマ特徴)を算出
ピッチクラスについては、一般的には、十二平均律の半音階 [C, C#, D, ... B] ごとに、オクターブでまとめたクロマ特徴を算出します。

音高特徴の算出
短時間フーリエ変換に基づく手法
時間波形 y を短時間フーリエ変換した信号の振幅 spec より、音高ー時間表現行列log_spec を算出します。
def compute_log_spectrogram(spec, freqs, tempo_ref=440, oct_bin=12, oct_num=7): offset = 4 * oct_bin - 3 # log_freqs[0] is corresponds to C1 (32.5 Hz) indices = np.arange(0, oct_bin*oct_num) log_freqs = tempo_ref * 2 ** ( (indices - offset) / oct_bin ) windows = gen_pitch_windows(freqs, log_freqs) log_spec = np.dot(windows, spec) return log_spec, log_freqs
ここで、配列 log_freqs には各音高の周波数が格納されています。処理としては、音高の値を取り出す窓関数行列 windows と spec の行列積を取ることで、音高ー時間表現を算出します
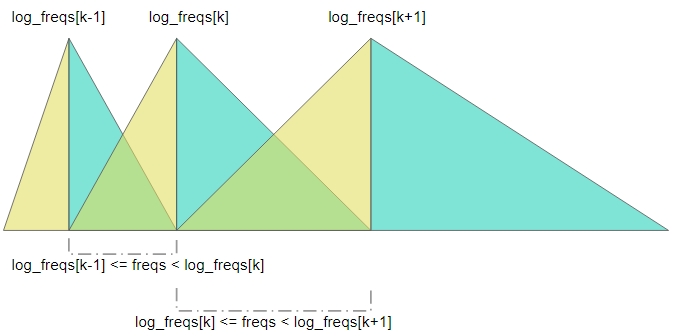
算出の際には、spec の各周波数ビンの値を、各音高にどのように分配(写像)するかが問題となります。様々な実装がありますが、例えば、MFCC を算出する際に使われるような三角窓を使うことが考えられます。
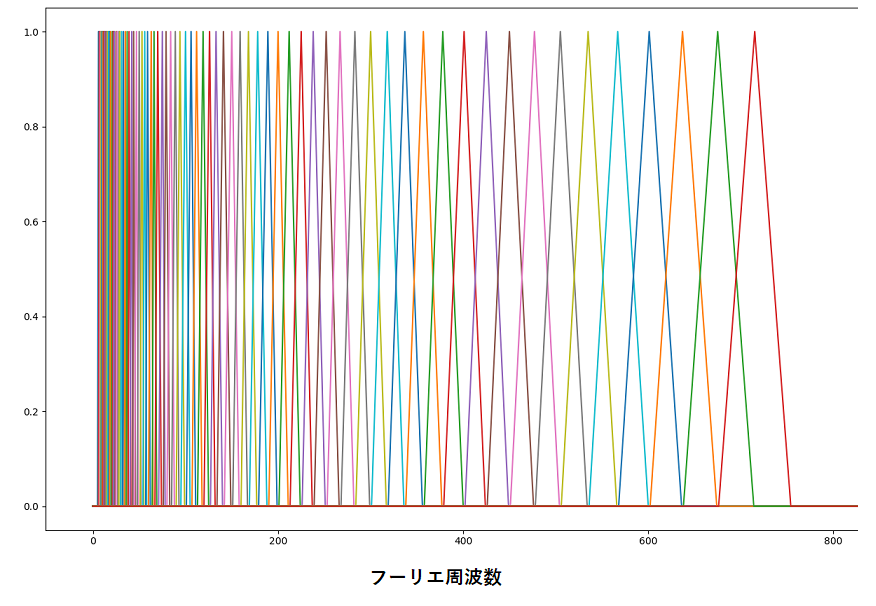
三角窓の場合では、各周波数ビンの値は2つの音高に分配されます。ただし、上の図のような三角窓だと、高周波数帯域ほどより多くの周波数ビンから値を集約するため、高周波数帯域の値が異常に大きくなってしまいます。
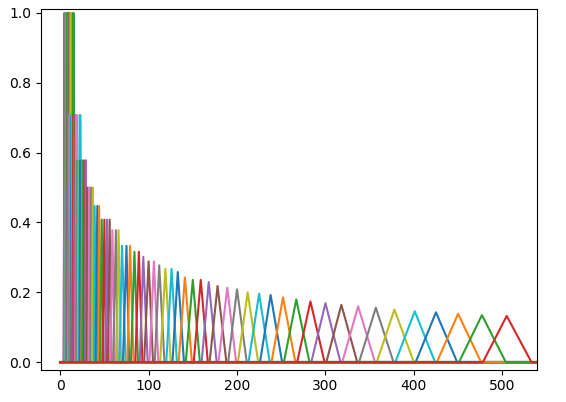
このような問題を回避するため、各対数周波数に対応する窓に重み付けすることが考えられます。例えば、以下のように高周波数帯域ほど窓の面積を小さくするのが一つの手です。
chroma_labels = ["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"] pitch_labels = [ c+str(p+1) for p in range(n_bins//12) for c in chroma_labels] filepath = "audio_example_pitch.mp3" y, sr = librosa.load(filepath, sr=16000, offset=95, duration=10) pitch, freqs = compute_logspec_from_stft(y, sr, hop_length, n_bins, n_fft=2048) plot_specgram(pitch, pitch_labels, "pitchgram", filepath=filepath, ticks=12)
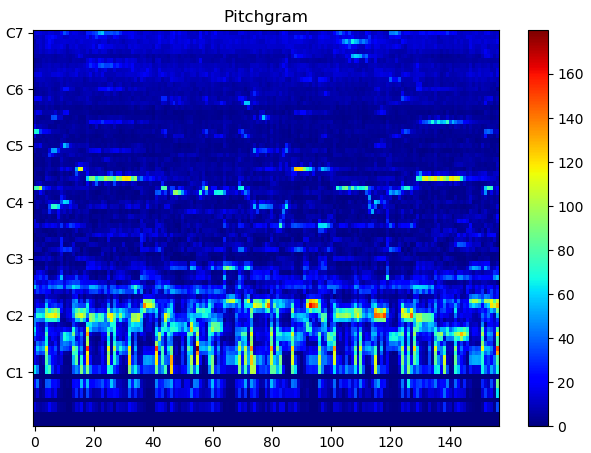
この手法の場合、短時間フーリエ変換の周波数解像度が低い(FFT窓幅が狭い)と、低周波数帯域ほど値がいい加減になりがちです。上記のプロットでは、B0などに値が上手く分配されていないことが分かります。
周波数解像度を上げようとすると計算量が増えるので、結局のところ、次に紹介する定Q変換を利用するのがよいと思います。
定Q変換 (CQT: Constant-Q Transform) に基づく手法
(定Q変換の紹介については、別途まとめます)
y, sr = librosa.load(filepath, sr=16000, offset=95, duration=10) n_bins = 84 hop_length = 1024 pitch = np.abs(librosa.cqt(y=y, sr=sr, hop_length=hop_length, n_bins=n_bins))
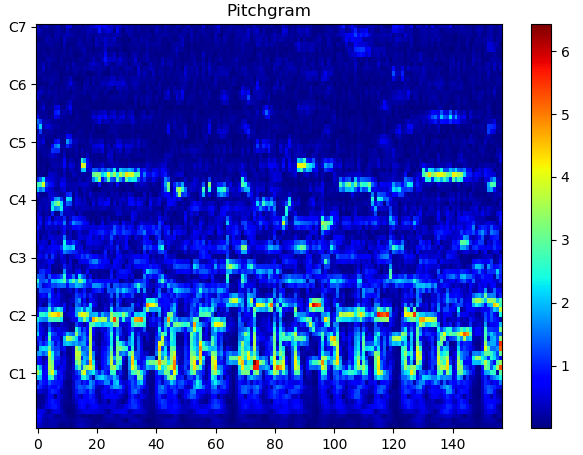
クロマ特徴の算出
音高ー時間表現行列 log_spec を、音高の軸でオクターブ(=12)おきに集約(平均)することで算出できます。
log_spec, log_freqs = compute_logspec_from_stft(y, sr, hop_length, n_bins, n_fft=n_fft) n_oct = 12 n_pitch, n_t = log_spec.shape chroma = np.zeros((n_oct, n_t)) for m in range(0, n_oct): chroma[m,:] = np.mean(log_spec[m:n_pitch:n_oct,:], axis=0)
LibROSAでは、librosa.core.cqt()に定Q変換した信号を引数として渡すことで、クロマ特徴を算出できます。もしくは、librosa.feature.chroma_cqt() に時間信号 y を渡して算出できます。
pitch = np.abs(librosa.cqt(y=y, sr=sr, hop_length=hop_length, n_bins=n_bins)) chroma = librosa.feature.chroma_cqt(C=pitch)
chroma = librosa.feature.chroma_cqt(y=y, sr=sr)

まとめ
コード、コード進行などの音楽分析でよく使われる、音高ー時間表現およびピッチクラスー時間表現(クロマ特徴)について紹介しました。
基本的には、LibROSA などのライブライの定Q変換を使うのが良いと思います(品質を上げるためのプリ・ポストプロセッシングも含まれるため)。 リアルタイム処理など計算量が少ないほうが良い場合は、STFTベースで算出する手法を実装してみるのがよいかもしれません。
補足
三角窓行列の算出コード (Python実装)
リニア周波数ビンの中心周波数配列 freqs[] と
対数周波数ビンの中心周波数配列 log_freqs[] に基づいて、shape==(len(log_freqs), len(freqs)) の三角窓の行列 windows を算出します
この実装では、図の黄色の部分を上昇直線 (ascend)、水色の部分を下降直線 (descend) として、分けて算出しています。
windows[k] /= np.sqrt(win_sample) は、各三角窓への重み付けを行っています。高周波数帯域では窓の幅が広くなるので、窓の面積を小さくしています。
注:log_freqs[] の最初と最後については、窓の算出方法はアバウトです(ちゃんとやろうとすると、それより外側の周波数が必要であるため)。
def gen_pitch_windows(freqs, log_freqs, weight_on=True): length, log_length = len(freqs), len(log_freqs) windows = np.zeros((log_length, length)) for k in range(0, log_length): win_sample = 0 # Descending linear line if k < log_length - 1: cond = np.logical_and(log_freqs[k] < freqs, log_freqs[k+1] >= freqs) else: cond = np.logical_and(log_freqs[k] < freqs, log_freqs[k] + (log_freqs[k]-log_freqs[k-1]) >= freqs) indices = np.where(cond)[0] if len(indices) == 0: pass elif len(indices) == 1: windows[k,indices[0]] = 1.0 win_sample += 1 else: descend = np.linspace(1.0, 0.0, len(indices)) windows[k, indices[0]-1:indices[-1]] = descend win_sample += len(descend) # Ascending linear line if k > 1: cond = np.logical_and(log_freqs[k-1] <= freqs, log_freqs[k] >= freqs) else: cond = np.array([]) indices = np.where(cond)[0] if len(indices) == 0: pass elif len(indices) == 1: windows[k,indices[0]] = 1.0 win_sample += 1 else: ascend = np.linspace(0.0, 1.0, len(indices)) windows[k, indices[0]:indices[-1]+1] = ascend win_sample += len(ascend) if weight_on and win_sample > 1: windows[k] /= np.sqrt(win_sample) """ plt.clf() plt.plot(windows.T) plt.show() """ return windows
*1:Singing Voice Separation with Deep U-Net Convolutional Networks
*2:音色については音響的な特徴として別途紹介します。