不協和度、緊張度に引き続き、“The Psychophysics of Harmony Perception: Harmony is a Three-Tone Phenomenon” より和音の明るさー暗さや嬉しさー悲しさを表すとされる和音のモダリティの算出モデルについて紹介します。
また、モダリティ曲線を算出するPythonのプログラムを紹介します。
モダリティの概要
モダリティは和音の緊張度と密接に結びついています。 前回紹介したの緊張度と音程の関係性より、増和音のような緊張度の高い和音から長三和音/短三和音に解決するということは、緊張度を作っている複数の音程の等しさが崩れることを意味します。
例えば、増三和音 C, E, G#の場合、第1,2音程はどちらも4半音です。
この状態を 4-4 と定義すると、例えば 4-3 に解決する場合は C, E, G、長三和音です。
一方、 Cを半音上げてC#とし 3-4 に解決する場合は C#, E, G#、短三和音となります。
従って、参考文献ではこのような複数の等しい音程の崩れが長/短三和音の解決感・響きを生成するという法則性をモデル化することで和音のモダリティ(明るいー暗い/嬉しいー悲しい)を表そうとしています。
純音のモダリティ曲線
不協和度、緊張度とモデルと同じく、まずは倍音のない純音のモデルを考えます。
純音の場合、以下の数式からモダリティを求めます。

x12, x23がそれぞれ第1,2音程であり、周波数比の対数を取ることで音程を線形な軸で扱います。
このモダリティの理論曲線は以下のようになっております。
すなわち、(第2音程 - 第1音程) が - 1 半音であればモダリティは正の値として長三和音(明るさ、嬉しさを示す)であり、+1 半音であればモダリティは負の値として短三和音(暗さ、悲しさを示す)というモデルになっています。
概要でも述べたように、このアイディアは緊張度で第1,2音程が等しくなることが元になっています。
そのため、実はモダリティを算出するモデルのexp関数の中身はほぼ緊張度の算出式と同じです*1。

なお、εはt123の値の大きさを調整する係数であり、論文ではε=1.56となっています。
以上をクラスとしてPythonで実装したのが以下になります。
注意点として、緊張度のモデルと同じく f1, f2, f3 は f1≦f2≦f3 であることが要求されます
class Modality(): def __init__( self, n_semitone=12, p=0.88 ): self.n_semitone = n_semitone self.p = p def calc_velocity(self, v1, v2, v3): return v1 * v2 * v3 def calc_pitch_distance(self, f1, f2): return np.abs(self.n_semitone * np.log2(f2/f1)) def calc_puretones(self, f1, f2, f3, v1, v2, v3, eps=1.56): x12 = self.calc_pitch_distance(f1, f2) x23 = self.calc_pitch_distance(f2, f3) v123 = self.calc_velocity(v1, v2, v3) m123 = - v123 * 2 * (x23-x12) / eps * np.exp( -( (x23-x12)/4 )**2 ) return m123
このコードを使い、3音の内の2音の音高を変えてプロットしました。
下図は音高がちょうど12平均律の各半音の時の値だけプロットしています。
f2とf3の入れ替えた結果は等しいため、対称的な形状となっています。

長/短三和音に該当するスロットでは、モダリティの値が大きく、もしくは小さくなっていることが分かります。
また、緊張度の結果と比べてみると、緊張度が高い三和音ではモダリティの値はほぼ0と算出されています。

倍音を考慮したモダリティ算出
次に、倍音を考慮したモダリティ M の算出を行います。
基本的には不協和度、緊張度の算出と同じ、3つの音の周波数比をN倍音まで全パターン足すことで算出します。
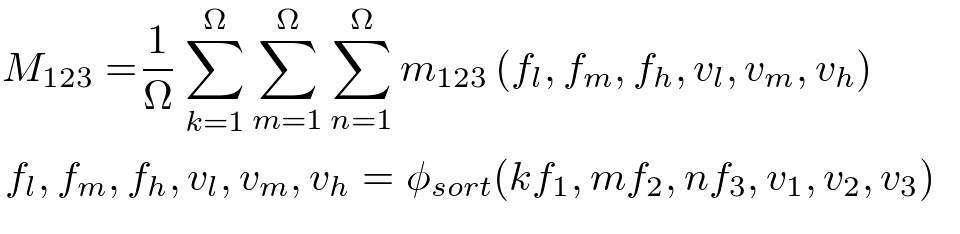
注意点としては、各緊張度 t を算出する際に渡す3つの音高はソートしてから渡す必要があります
Python実装は、先ほどのModalityクラスにメソッドを追加しました。
def calc(self, f1, f2, f3, v1=1.0, v2=1.0, v3=1.0, n_overtones=1): M123 = 0.0 f, v = np.zeros(3), np.zeros(3) for k in range(1, n_overtones+1): for m in range(1, n_overtones+1): for n in range(1, n_overtones+1): f[:] = f1 * k, f2 * m, f3 * n v[:] = v1*(self.p**(k-1)), v2*(self.p**(m-1)), v3*(self.p**(n-1)) args = np.argsort(f) f[:], v[:] = f[args], v[args] M123 += self.calc_puretones(f[0], f[1], f[2], v[0], v[1], v[2]) return M123 / n_overtones def surface(self, f_lower, f_centers, f_uppers, v1=1.0, v2=1.0, v3=1.0, n_overtones=1): M_mx = np.zeros((f_centers.shape[0], f_uppers.shape[0])) for k, fc in enumerate(f_centers): for m, fu in enumerate(f_uppers): M_mx[k,m] = self.calc(f_lower, fc, fu, v1, v2, v3, n_overtones) return M_mx
なお、緊張度の場合と同じく、このコードはナイーブな実装のため3重ループが出てきており計算速度は遅いです。
高速化のためには、例えば Numba などを使って実装するのがよいと思われます。
以下が計算する倍音数の上限値 n_orvertonesを変えたときの結果です。
計算する倍音数を大きくすると倍音の影響でモダリティ曲線(曲面)が変化することが分かります。
■2倍音まで計算

■3倍音まで計算

■4倍音まで計算

■6倍音まで計算

プロット用コード
まとめ
Pythonで和音のモダリティ(明るいー暗い/嬉しいー悲しい)を算出するモダリティ曲線 (Modality Curve) を実装しました。
不協和度、緊張度と合わせて使うことで、和音、和音進行、ヴォイシングの分析や検出に利用できると考えられます。
参考文献
- Fujisawa, Takashi. (2006). The Psychophysics of Harmony Perception: Harmony is a Three-Tone Phenomenon. Empirical Musicology Review. 1. 10.18061/1811/24080.
- 藤沢隆史, ノーマン D. クック, "和音性の計算法と曲線の描き方 : 不協和度・緊張 度・モダリティ",2006.
*1:緊張度のモデルとは分母の係数の値が異なることに注意