データをクラスタリングするアルゴリズムの代表的な手法の一つとして,K-means (k平均法)が知られています.
シンプルな動作原理でクラスタリングできるので取っつきやすく,また,新たな仮定や制約を追加することで様々な派生アルゴリズムが提案されてきました.
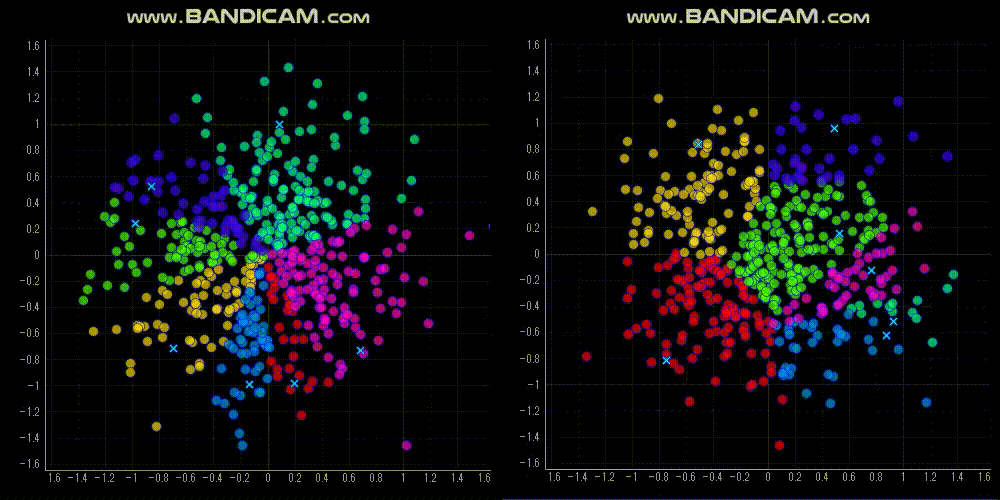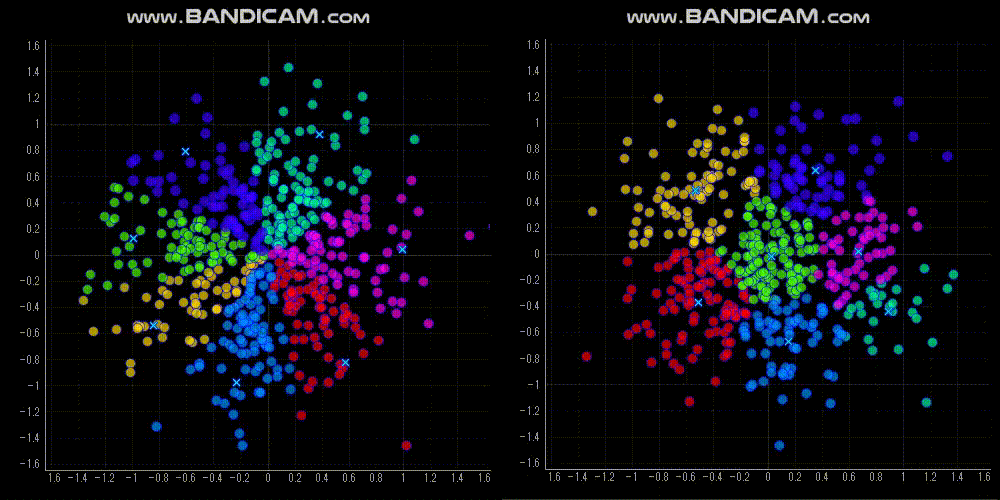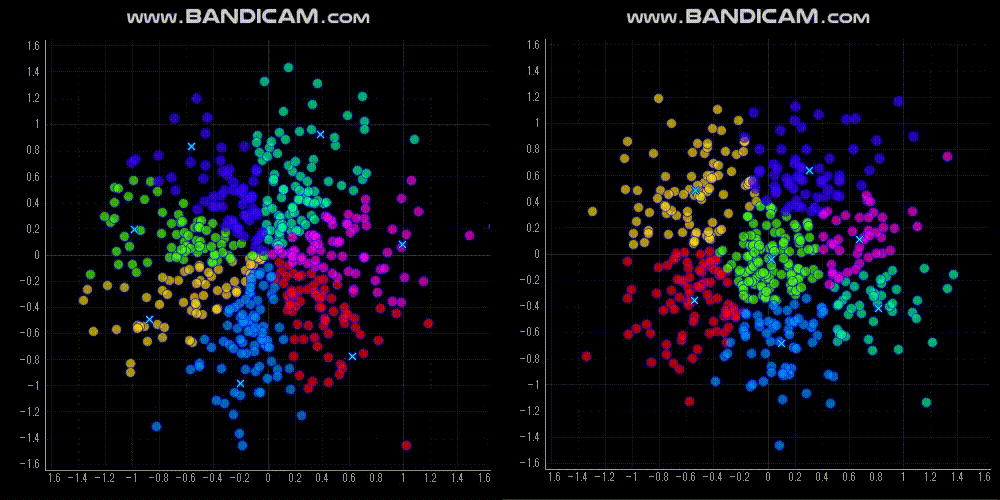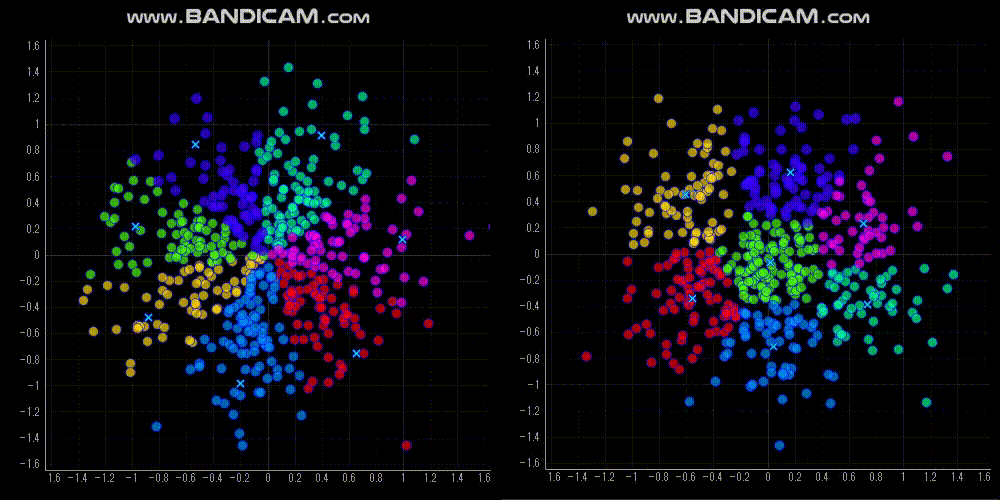
今回は,「原点からの方向(角度)でクラスタリングする」という制約でクラスタリングする Spherical K-means を紹介します.
K-meansの実装
使うデータ
- クラスタリングするデータ:
x.shape==(サンプル数, 特徴量次元数) - ↑の各サンプルがどのクラスタに属すか:
labels.shape==(サンプル数, ラベル数) - クラスタ重心:
centroids.shape==(ラベル数, 特徴量次元数)
xは予め用意する必要があります.
また,centroidsもしくはlabelsの初期値を設定する必要があります.
実装の流れ
centroidsの初期値を設定するパターンです.
centroids初期値を設定- 反復処理
反復処理は,反復回数を設定したり,サンプルの所属クラスタ重心との距離の総和/平均値が一定値以下で反復を止めるようにします.
Spherical K-means の実装方法
初期値計算
特徴量の次元をNとすると,Spherical K-means の重心はN次元空間の単位超球面上に位置します.2次元だと,単位円上です.
なので,単位円上でクラスタ重心がなるべくバラバラになるように初期値を設定しました.
注意として,データにもよりますが,単位超球面上外の値をセットすると,反復すると無意味解(原点)になることがありました.
def calc_init_centroids_cos(centroids, n_labels): for k in range(n_labels): theta = np.random.random(1)*2*np.pi centroids[k,0] = np.cos(theta) centroids[k,1] = np.sin(theta)
各サンプルとクラスタ重心との距離計算
def distance_cos(x, v)
return 1.0 - np.dot(x, v)
クラスタ重心の更新
あるクラスタに所属するデータにおいて、平均値をそのノルムで割ることで単位超球面上の重心を算出します.
def calc_centroid_cos(x, v, m): v[m] = np.sum(x, axis=0) v[m] /= np.linalg.norm(v[m]) + 1e-15
使いどころ
データの特徴量次元が大きくなると,次元に呪われて*1通常のK-meansでは使い物にならない結果となることが多々あります.
通常であれば次元削減が良い方針ですが,高次元データのまま分析したいケースも割とあったりします.
そんな時,Spherical K-meansであればは高次元のデータでも意味のあるクラスタリングを得られる可能性があります.
ソースコード
pyqtgraph-app/pqg_spherical_kmeans.py at main · Kurene/pyqtgraph-app · GitHub
