Python LibROSA で音楽・歌声（ボーカル）をピッチシフト librosa.effects.pitch_shift()

まえがき

ボーカルや楽器の録音データに対して、

「音の長さを変えずに、音の高さを変えたい」

と思うことはありませんか？

この処理はピッチシフト*1と呼ばれていて、

• 移調/転調
• ハモり／コーラスパートの生成
• 音の高さの修正

といったエフェクターやDAWでの処理で利用されています。

Pythonの音楽分析モジュール LibROSA にはピッチシフトを簡単に実行できる関数が用意されているため、簡単に紹介したいと思います。

librosa.effects.pitch_shift() の使い方

引数について

librosa - librosa.effects.pitch_shift

librosa.effects.pitch_shift(y, sr, n_steps, bins_per_octave=12, res_type='kaiser_best', **kwargs)

重要な引数は以下の通りです。

• y: np.ndarray型の、時間波形領域の入力信号です。ver. 0.8.0 時点では、1次元配列、すなわちモノラルの信号のみを対象としています。
• sr: サンプリング周波数
• n_steps: float型であり、どのくらい周波数をシフトさせるかを指定する引数です。
• bins_per_octave: float型であり、オクターブのビン数（１オクターブ内に音程がいくつあるか）を指定します。

なお、中身はlibrosa.effects.pitch_shift()の正体はフェーズボコーダであり、そのパラメタ（STFTフレーム長など）も引数として指定することができます。

フェーズボコーダにご興味がありましたら、以下の記事も合わせてご覧ください。

www.wizard-notes.com

半音単位のピッチシフト

基本的な使い方として、まず半音単位のピッチシフトを説明します。

n_stepsの値を変更することで、音の高さをどのくらい上げ下げするのか制御します。

具体的には、このn_stepsによって、オクターブ（周波数比2：1）に対してどのくらいシフトさせるかを決めることになります。

デフォルト値のようにbins_per_octave=12であれば、n_stepsが1増えるごとに、1半音上がるということになります。

例：

• 1オクターブ上: n_steps=12
• 1オクターブ下: n_steps=-12
• 完全5度上（半音7個分）: n_steps=7
• 完全4度上（半音5個分）: n_steps=5

このように、元の音源をN半音を上げ下げするような音波音単位のピッチシフトはn_stepsに整数値を設定すればOKです*2。

周波数を指定するピッチシフト

応用的な使い方として、周波数を指定したピッチシフトを説明します。

具体的には，「10Hzほど音の高さを上げたい」というような、基本周波数（音高）をどれくらいシフトするのかを指定するピッチシフトです。

ピッチシフト前と後の基本周波数をそれぞれFo, Fo_shiftとすると、以下の関係が成立します。

Fo_shift = Fo * 2.0 ** (n_steps/bins_per_octave)
(**はべき乗)

n_steps / bins_per_octave = log2 (Fo_shift / Fo)

簡単化のためbins_per_octave=1とすると、

n_steps = log2 (Fo_shift / Fo)

となり、ピッチシフト前後の周波数比に対して2を底とする対数を取ることでn_stepsの値を求めることができます。

使い方のサンプル

プロット

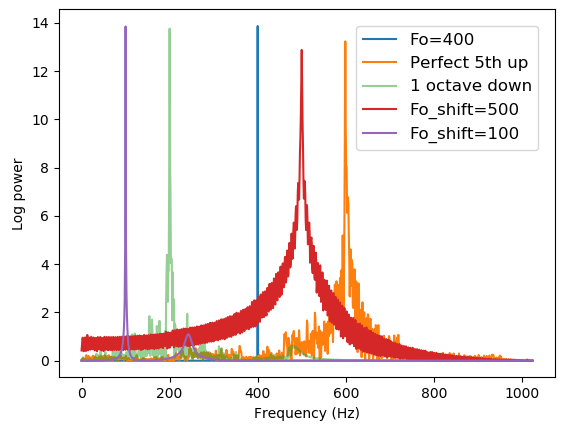
コード

import librosa
import numpy as np
import matplotlib.pyplot as plt

sr = 2048 #librosa.phase_vocoderのn_fft=2048 なので
Fo = 400
eps = 1.0
x = np.arange(0, sr)/sr
y  = np.sin(2.0 * np.pi * Fo * x)

n_fft = len(y)

# 元波形
plt.plot(np.log(np.abs(np.fft.fft(y))**2+eps)[0:n_fft//2+1], label=f"Fo={Fo}")


# 完全5度上
label = "Perfect 5th up"
y_shift = librosa.effects.pitch_shift(y, sr, n_steps=7)
plt.plot(np.log(np.abs(np.fft.fft(y_shift))**2+eps)[0:n_fft//2+1], label=label)

# オクターブ下
label = "1 octave down"
y_shift = librosa.effects.pitch_shift(y, sr, n_steps=-12)
plt.plot(np.log(np.abs(np.fft.fft(y_shift))**2+eps)[0:n_fft//2+1], label=label, alpha=0.5)

# ピッチシフト後の周波数指定
Fo_shift = 500
n_steps = np.log2(Fo_shift / Fo)
label = f"Fo_shift={Fo_shift}"
y_shift = librosa.effects.pitch_shift(y, sr, n_steps=n_steps, bins_per_octave=1)
plt.plot(np.log(np.abs(np.fft.fft(y_shift))**2+eps)[0:n_fft//2+1], label=label)

Fo_shift = 100
n_steps = np.log2(Fo_shift / Fo)
label = f"Fo_shift={Fo_shift}"
y_shift = librosa.effects.pitch_shift(y, sr, n_steps=n_steps, bins_per_octave=1)
plt.plot(np.log(np.abs(np.fft.fft(y_shift))**2+eps)[0:n_fft//2+1], label=label)


plt.xlabel("Frequency (Hz)")
plt.ylabel("Log power")
plt.legend(loc='upper right', borderaxespad=1, fontsize=12)
plt.show()

※STFT窓長とプロットの都合上、サンプリング周波数を2048にしています。

注意

librosa.effects.pitch_shift()で使われているフェーズボコーダlibrosa.phase_vocoderはナイーブな実装であるため、特にピッチを上げるピッチシフトでは音質が劣化しやすい傾向があります。 従って、実用時には注意が必要です。

librosa.phase_vocoderのドキュメントには、 RubberBand libraryのPythonラッパーであるpyrubberbandモジュールの利用が推奨されています。

補足：ピッチシフトはタイムストレッチ？

実は、librosa.effects.pitch_shift()のコードを見てみると、

def pitch_shift(y, sr, n_steps, bins_per_octave=12, res_type="kaiser_best", **kwargs):
    ...
    # Stretch in time, then resample
    y_shift = core.resample(
        time_stretch(y, rate, **kwargs), float(sr) / rate, sr, res_type=res_type
    )
    ...

実は、ピッチシフト（カラオケの転調）はタイムストレッチ＋リサンプリングで実現できることが分かります。

もしタイムストレッチの方にもご興味ありましたら、以下の記事も合わせてご覧ください。

www.wizard-notes.com

*1:エフェクトとしてのピッチシフトは、対数周波数領域でのシフトであり倍音の周波数比は保持されるため、音楽的に調和した信号が出力されます。一方で、例えばどの倍音も100Hzだけ上下する、つまり線形周波数領域でのシフトは、音楽的に調和しなくなります。

*2:微分音の場合、例えば四分音上げる場合はn_steps=0.5とすることで対応できます